Предмет: Алгебра, автор: PurPon

Помогите пожалуйста с 3 и 4 номером обеих вариантов.
Пожалуйста с решением.

Приложения:

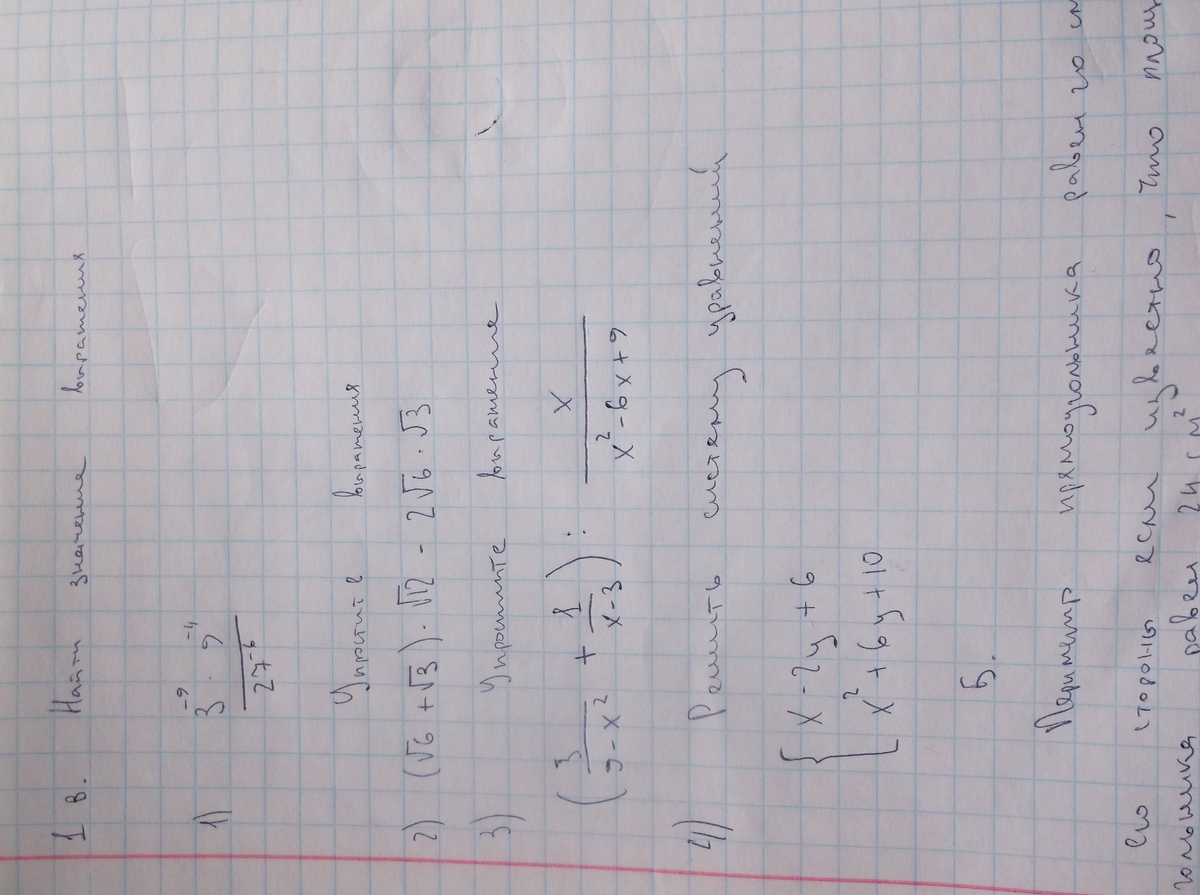
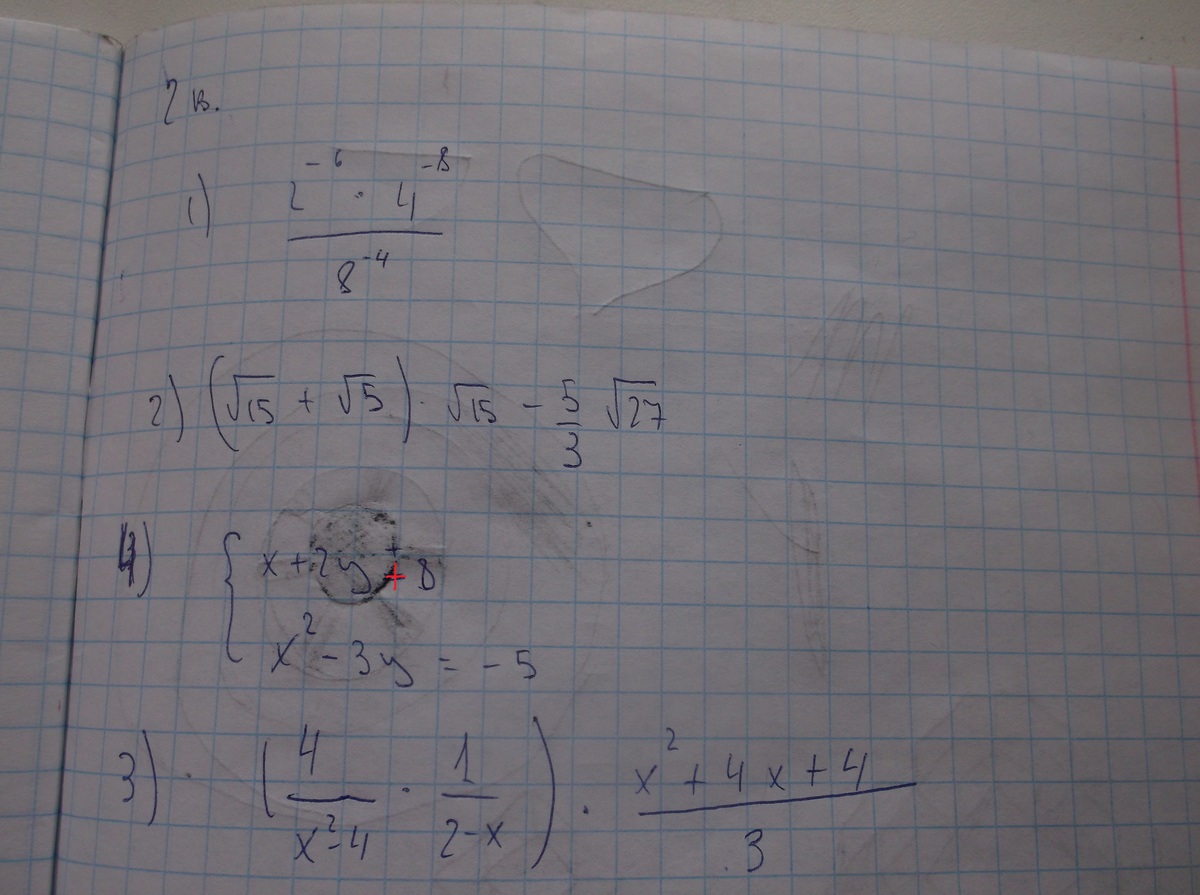
sangers1959: В номере 4 где знаки равенства?

PurPon: Там их нет

sangers1959: Хорошо, будем считать,что уравнения равны 0.

PurPon: Там = 10

PurPon: В 4-ом не +10 , =10

sangers1959: ДА, я уже разобрался. Сейчас будет решение.

PurPon: Воу, жду с нетерпением :)

sangers1959: А номер 3 делать?

PurPon: Да)

PurPon: Можно обеих вариантов

Ответы

Автор ответа: sangers1959

4.
x-2y=6 I*3 3x-6y=18 Суммируем эти уравнения:
x²+6y=10 x²+6y=10 x²+3x=28 x²+3x-28=0 D=121
x₁=4 x₂=-7.
y₁=-1 y₂=-6,5
3. Рассмотрим множитель, который слева:
=(-3/((x-3)(x+3))+1=(-3+(x+3))/(([+3)(x-3))=x/((x-3)(x+3))
Рассмотрим множитель, который справа:
=x/(x-3)²
теперь произведём деление множителей:
x*(x-3)²/((x*(x-3)(x+3))=(x-3)/(x+3).
1. 3⁻⁹*3⁻⁴/27⁻⁶=3⁻¹³/(3³)⁻⁶=3-¹³/3⁻¹⁸=3⁵=243.
2. (√6+√3)*√12-2*√6*√3=√72+√36-2√18=√(36*2)+6-2*√(9*2)=
=√36*√2+6-2*√9*√2=6√2+6-6√2=6.
Вариант 2.
1. 2⁻⁶*4⁻⁸/8⁻⁴=2⁻⁶*(2²)⁻⁸/(2³)⁻⁴=2⁻⁶*2⁻¹⁶/2⁻¹²=2⁻²²/2⁻¹²=2⁻¹°.
2. (√15+√5)*√15-(5/3)*√27=15+√75-(5/3)/√(9*3)=15+√(3*25)-(5/3)*3*√3=
=15+5*√3-5*√3=15.

sangers1959: Второй вариант делать?

PurPon: Спасибо, а можно сделать оба варианта под 1 и 2?

sangers1959: Можно.Делаю 1 вариант 1 и 2.

sangers1959: Во втором варианте делать все 4 задания?

PurPon: Нет, можно 1 и 2?

sangers1959: Хорошо.

sangers1959: Больше помощь не нужна?

PurPon: Воу, спс, нужна, можно ещё 1 и 2 другого варианта

sangers1959: Так я уже написал решение Вариант 2, 1 и 2 задание.

sangers1959: Есть? В самом конце?

Предыдущий вопрос

Следующий вопрос