Предмет: Алгебра,
автор: Стефания98
Пожалуйста помогите решать((((
Приложения:
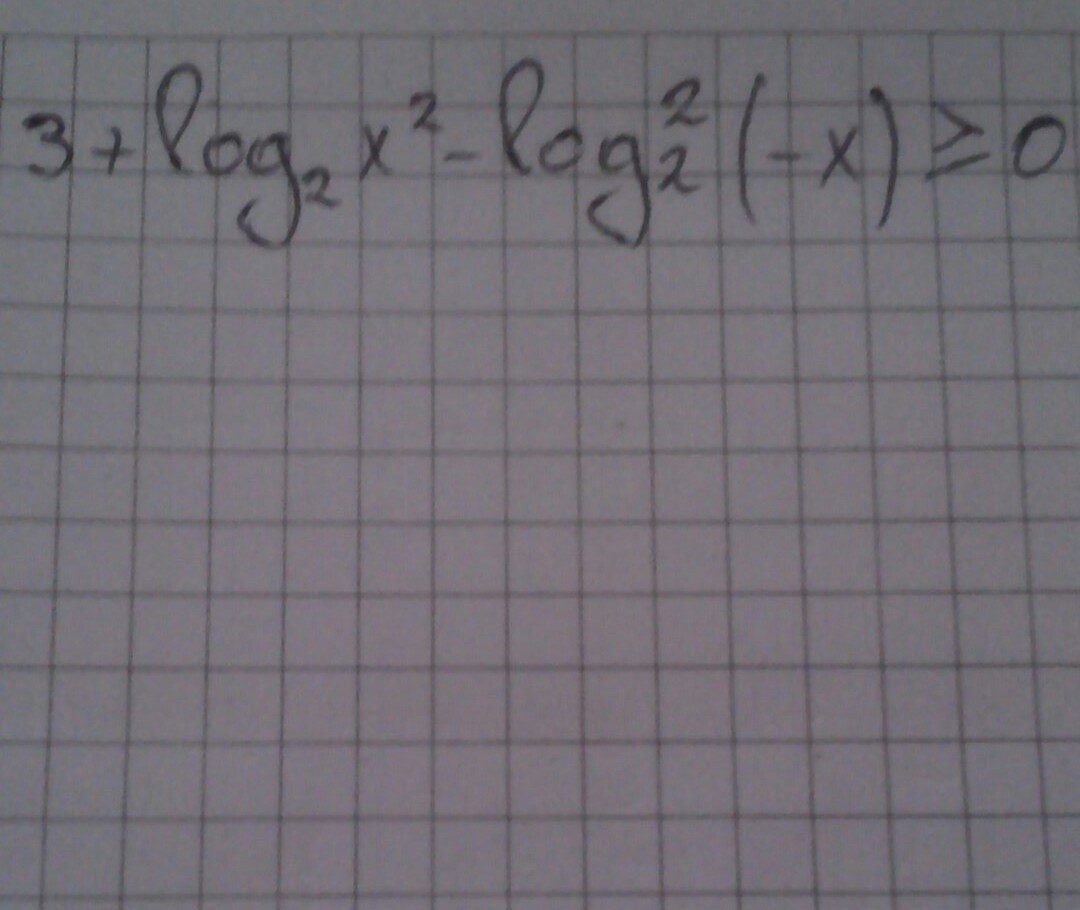
Ответы
Автор ответа:
0
найдем ОДЗ:
-x >0

общее решение ( - ∞; 0)




введем замену

D=4+12=16
t1=3
t2= - 1
решаем методом интервалов

![[tex]log_{2} \frac{1}{2} \leq log_{2} (-x) \leq log_{2} 8[ [tex]log_{2} \frac{1}{2} \leq log_{2} (-x) \leq log_{2} 8[](https://tex.z-dn.net/?f=%5Btex%5Dlog_%7B2%7D+%5Cfrac%7B1%7D%7B2%7D+%5Cleq+log_%7B2%7D+%28-x%29+%5Cleq+log_%7B2%7D+8%5B)


учитывая ОДЗ, получаем ответ:
[ - 3; - ]
]
-x >0
общее решение ( - ∞; 0)
введем замену
D=4+12=16
t1=3
t2= - 1
решаем методом интервалов
учитывая ОДЗ, получаем ответ:
[ - 3; -
Похожие вопросы
Предмет: Русский язык,
автор: мадина525
Предмет: Окружающий мир,
автор: delyacat7015
Предмет: Русский язык,
автор: ivbugaev2000
Предмет: Математика,
автор: DoktorBGTY
Предмет: Математика,
автор: viktoriabucha90