Предмет: Геометрия,
автор: Hshshahga
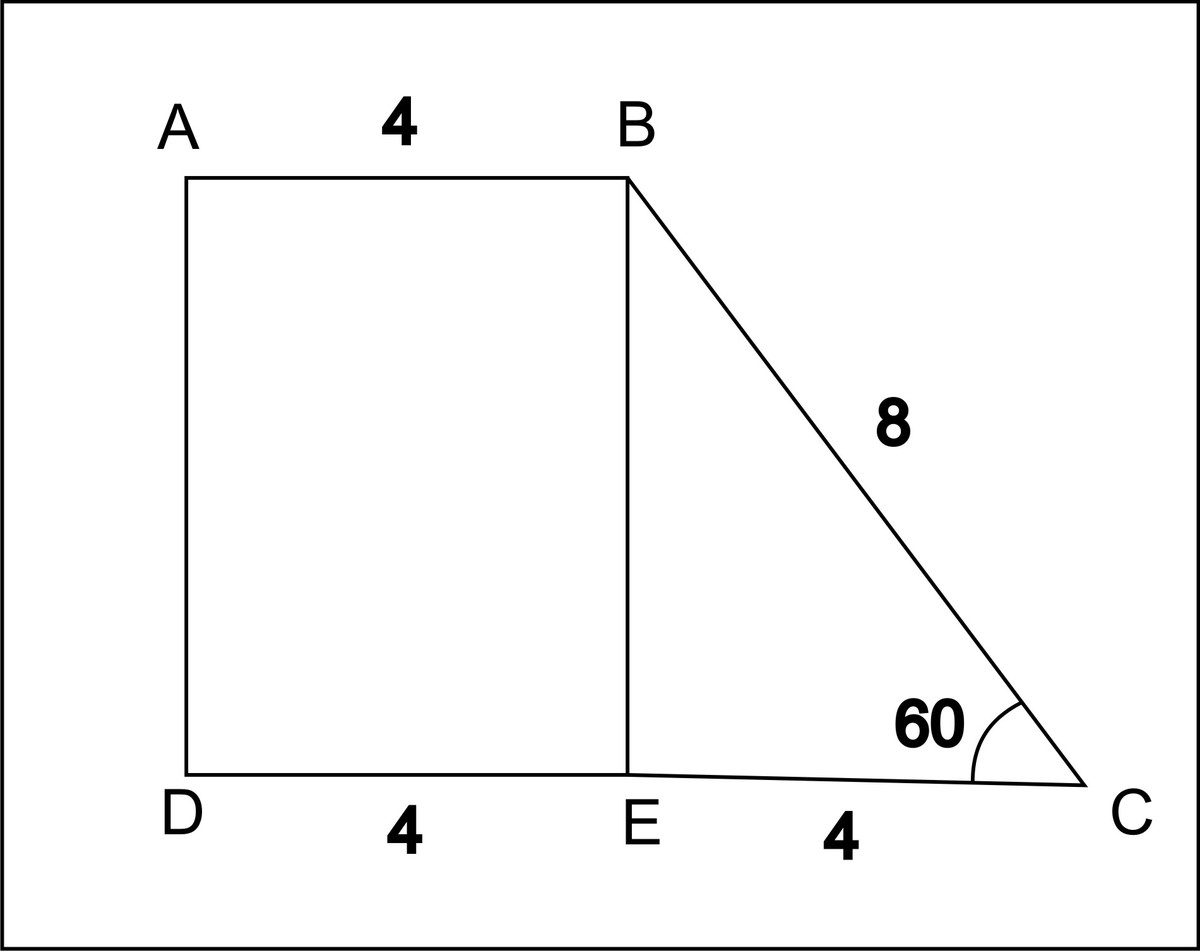
Найти объём тела полученного при вращении прямоугольной трапеции с острым углом 60 градусов меньшим основанием 4 ,больше боковой стороной стороной 8м вокруг:а)меньшим основанием,б)большим основанием.
Ответы
Автор ответа:
1
ЕС=ВС·cos60=8/2=4
DE=AB=4
AD=BC·sin60=(√3·8)/2=4√3
а)при нахождении объема тела полученного при вращении вокруг меньшего основания трапеции мы возьмём объём цилиндра с высотой 8 и вычтем объём конуса с высотой 4
V(цилиндра)=πR²·H
V(конуса)=(1/3)πR²·H
V(тела)=π(4√3)²·4+(1/3)·π·(4√3)²·4=256π
б)при нахождении объема тела полученного при вращении вокруг большего основания трапеции мы возьмём объём цилиндра с высотой 4 и прибавим объём конуса с высотой 4
V(тела)=π(4√3)²·8-(1/3)·π·(4√3)²·4=320π
DE=AB=4
AD=BC·sin60=(√3·8)/2=4√3
а)при нахождении объема тела полученного при вращении вокруг меньшего основания трапеции мы возьмём объём цилиндра с высотой 8 и вычтем объём конуса с высотой 4
V(цилиндра)=πR²·H
V(конуса)=(1/3)πR²·H
V(тела)=π(4√3)²·4+(1/3)·π·(4√3)²·4=256π
б)при нахождении объема тела полученного при вращении вокруг большего основания трапеции мы возьмём объём цилиндра с высотой 4 и прибавим объём конуса с высотой 4
V(тела)=π(4√3)²·8-(1/3)·π·(4√3)²·4=320π
Приложения:


Похожие вопросы
Предмет: Английский язык,
автор: samiasergibaeva
Предмет: Русский язык,
автор: alinurkanat
Предмет: Русский язык,
автор: ibragimgadjizad
Предмет: Английский язык,
автор: valdemar85
Предмет: Русский язык,
автор: hdjfjfbchfhfy