Предмет: Геометрия,
автор: PStolichnaya
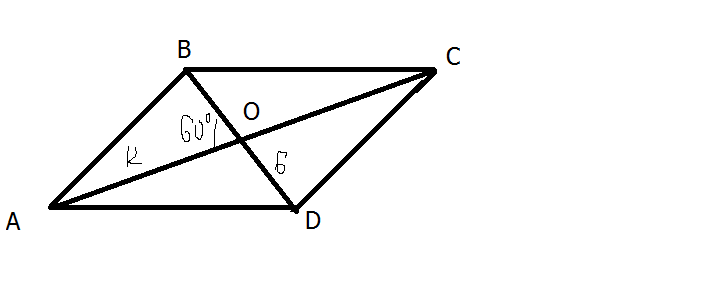
В параллелограмме ABCD диагонали AC=12 м, BD=6 м, угол AOB=60 градусов. Найти периметр параллелограмма.
Тема: Теорема синусов. Теорема косинусов.
Ответы
Автор ответа:
0
1) Рассмотрим ΔABO, по свойству параллелограмма BO=OD и AO=OC тогда BO=3 AO=6
по теореме косинусов
2) Рассмотрим ΔBOC, BO=3, OC=6, <BOC=180-<AOB <BOC=120(как смежные),
по теореме косинусов
3) По свойству параллелограмма AB=CD , BC=AD, P=AB+BC+CD+AD
Приложения:
Похожие вопросы
Предмет: Физика,
автор: Art121206
Предмет: Информатика,
автор: andreibogaev
Предмет: Литература,
автор: bodnarovskaolga4
Предмет: Алгебра,
автор: Аноним
Предмет: Геометрия,
автор: Проффесор