Question

биссектрисы углов а и д параллелограмма авсд пересекаются в точке м, лежащей на стороне ВС. Докажите, что точка м равноудалена от прямых АВ, АД и СД

Answer 1

  Любая точка биссектрисы угла равноудалена от его сторон.
Точка М лежит на пересечении биссектрис АМ и ДМ.
Следовательно. точка М равноудалена от прямых АВ, АД и СД. 
В данной задаче не стоит вопрос о доказательстве теоремы, утверждающей равенство расстояний от точки на биссектрисе до ее сторон.
Кратко.
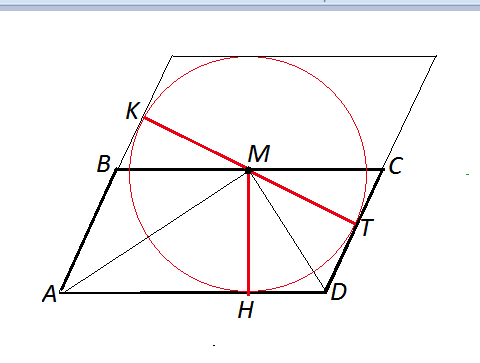
Продолжив стороны параллелограмма до равенства всех его сторон, . получим ромб 
Точка М, являясь пересечением биссектис углов. станет центром  вписанной в ромб окружности. (см.рисунок в приложении). Ее радиусы в точки касания перпендикулярны прямым, содержащим стороны параллелограмма и являются расстоянием от М до прямых, содержащих стороны параллелограмма. Радиусы окружности равны, следовательно, расстояния от М до прямых АВ, АД и СД равны, что и требовалось доказать.