Предмет: Математика,
автор: Shramman
cos(п/4+t)cos(п/12-t)-cos(п/4-t)cos(5п/12+t)
Ответы
Автор ответа:
16
1. С помощью формулы приведения для второго слагаемого, т.е.:
cos (pi/4 - t) = sin (pi/2-(pi/4-t)) = sin (pi/4+t)
cos (5*pi/12 + t) = sin(pi/2 - (5*pi/12+t) = sin (pi/12-t)
Подставляем в условие:
cos (pi/4 + t)*cos (pi/12 - t)-cos (pi/4 - t)*cos (5*pi/12 + t) = cos (pi/4 + t)*cos (pi/12 - t) - sin (pi/4+t)*sin (pi/12-t)
2: формулу с фото написать сюда
Где в качестве альфа = pi/4 + t, бета = pi/12-t
3: Получаем: cos (альфа + бета) = cos (pi/4 + t + pi/12-t) = cos (pi/4 + pi/12) = cos (4*pi/12) = cos (pi/3) = 1/2
cos (pi/4 - t) = sin (pi/2-(pi/4-t)) = sin (pi/4+t)
cos (5*pi/12 + t) = sin(pi/2 - (5*pi/12+t) = sin (pi/12-t)
Подставляем в условие:
cos (pi/4 + t)*cos (pi/12 - t)-cos (pi/4 - t)*cos (5*pi/12 + t) = cos (pi/4 + t)*cos (pi/12 - t) - sin (pi/4+t)*sin (pi/12-t)
2: формулу с фото написать сюда
Где в качестве альфа = pi/4 + t, бета = pi/12-t
3: Получаем: cos (альфа + бета) = cos (pi/4 + t + pi/12-t) = cos (pi/4 + pi/12) = cos (4*pi/12) = cos (pi/3) = 1/2
Приложения:
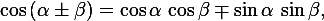
Shramman:
Большое спасибо.
Похожие вопросы
Предмет: Другие предметы,
автор: grendycraft
Предмет: Английский язык,
автор: dfjjrrjsoodkljv
Предмет: Английский язык,
автор: Lera5567689
Предмет: Алгебра,
автор: anna611975
Предмет: Литература,
автор: 135957