Предмет: Алгебра,
автор: alexandrovna99
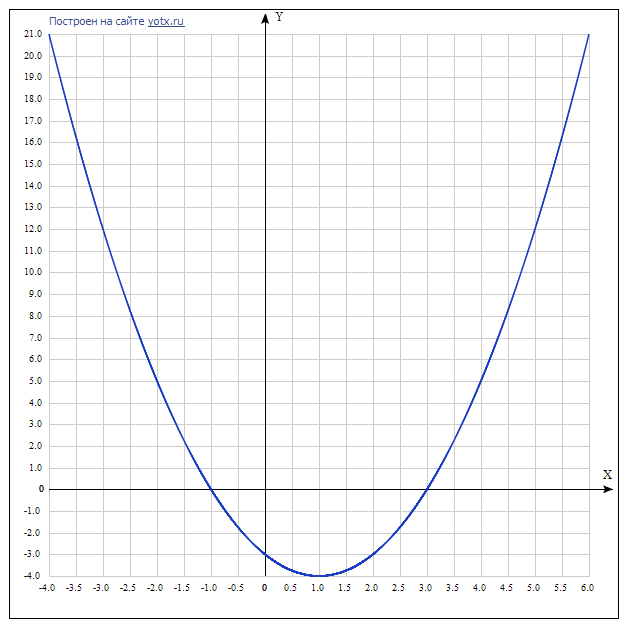
Побудуйте графік функції у=х(квадрат) - 2х - 3. Користуючись графіком установіть:
1.проміжок, на яком функція зростає
2. множину розв`язків нерівності х (квадрат) -2х-3 > 0
Ответы
Автор ответа:
24
График заданной функции - парабола.
Так как коэффициент при х² положителен (он равен 1), то ветви параболы направлены вверх.
Вершина параболы, представленной в виде у=ах+ву+с, определяется из выражения Хо = -в / 2а = -(-2) / 2*1 = 2/2 = 1.
После этого можно ответить на заданные вопросы:
1.проміжок, на яком функція зростає - (1,00).
2. множину розв`язків нерівності х (квадрат) -2х-3 > 0:
для этого надо решить уравнение х² - 2х - 3 = 0, чтобы найти точки пересечения графиком оси х.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-2)^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁ = (√16-(-2))/(2*1)=(4-(-2))/2=(4+2)/2=6/2 = 3;
x₂ = (-√16-(-2))/(2*1)=(-4-(-2))/2=(-4+2)/2=-2/2 = -1.
Отсюда ответ: -1 < x >3.
Для построения графика нужны координаты точек:
xy-4.0 21 -3.5 16.25 -3.0 12 -2.5 8.25 -2.0 5 -1.5 2.25 -1.0 0 -0.5 -1.75 0 -3 0.5 -3.75 1.0 -4 1.5 -3.75 2.0 -3 2.5 -1.75 3.0 0 3.5 2.25 4.0 5 4.5 8.25 5.0 12 5.5 16.25 6.0 21
Так как коэффициент при х² положителен (он равен 1), то ветви параболы направлены вверх.
Вершина параболы, представленной в виде у=ах+ву+с, определяется из выражения Хо = -в / 2а = -(-2) / 2*1 = 2/2 = 1.
После этого можно ответить на заданные вопросы:
1.проміжок, на яком функція зростає - (1,00).
2. множину розв`язків нерівності х (квадрат) -2х-3 > 0:
для этого надо решить уравнение х² - 2х - 3 = 0, чтобы найти точки пересечения графиком оси х.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-2)^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x₁ = (√16-(-2))/(2*1)=(4-(-2))/2=(4+2)/2=6/2 = 3;
x₂ = (-√16-(-2))/(2*1)=(-4-(-2))/2=(-4+2)/2=-2/2 = -1.
Отсюда ответ: -1 < x >3.
Для построения графика нужны координаты точек:
xy-4.0 21 -3.5 16.25 -3.0 12 -2.5 8.25 -2.0 5 -1.5 2.25 -1.0 0 -0.5 -1.75 0 -3 0.5 -3.75 1.0 -4 1.5 -3.75 2.0 -3 2.5 -1.75 3.0 0 3.5 2.25 4.0 5 4.5 8.25 5.0 12 5.5 16.25 6.0 21
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: кок51
Предмет: Українська мова,
автор: LolyMou
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним