Предмет: Алгебра,
автор: cukerka
Помогите доказать задачу на комплексные числа:
Приложения:
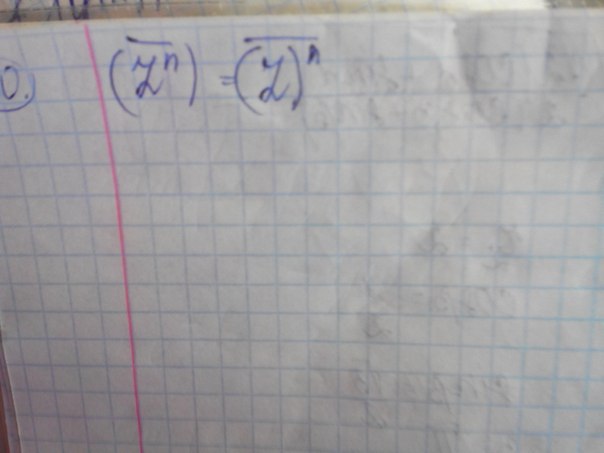
Ответы
Автор ответа:
1
Пусть  , тогда спряженное число равно
, тогда спряженное число равно

По формуле Муавра для комплексных чисел

справедливо равенство

(а также используя четность косинуса и нечетность синуса
 )
)
имеем

что и требовалось доказать.
Доказано
По формуле Муавра для комплексных чисел
справедливо равенство
(а также используя четность косинуса и нечетность синуса
имеем
что и требовалось доказать.
Доказано
cukerka:
Спасибо огромное, всё понятно
Похожие вопросы
Предмет: Русский язык,
автор: ViD111
Предмет: Английский язык,
автор: KaterinaPiers
Предмет: Українська мова,
автор: MASHA28788
Предмет: Алгебра,
автор: kirill33556
Предмет: Алгебра,
автор: bbfd3t89kf