Предмет: Геометрия,
автор: Marisabel10061999
Найдите площадь треугольника АВС,если известны координаты его вершин:
а) А(4;-1;2),В(-1;2;4),С(2;4;-1)
б)А(2;1;2),В(2;2;1),С(2;2;2)
Ответы
Автор ответа:
2
расстояние между двумя точками в пространстве находится по формуле
АВ=√((хb-xa)²+(yb-ya)²+(zb-za)²)
а)AB=√((-1-4)²+(2+1)²+(4-2)²)
AB=√(25+9+4)=√38
BC=√((2+1)²+(4-2)²+(-1-4)²)=√(9+4+25)=√38
AC=√((2-4)²+(4+1)²+(-1-2)²=√(4+25+9)=√38
AB=BC=AC
треугольник равносторонний все углы 60
высота треугольника Н=АВ·сos30=√38·((√3)/2)=(√114)/2
S(ABC)=H·AC·(1/2)=((√114)/2)·√38·(1/2)=(19√3)/2
б)АВ=√(0+(2-1)²+(1-2)²=√2
АС=√(0+(2-1)²+0)=1
СВ=√(0+0+(1-2)²)=1
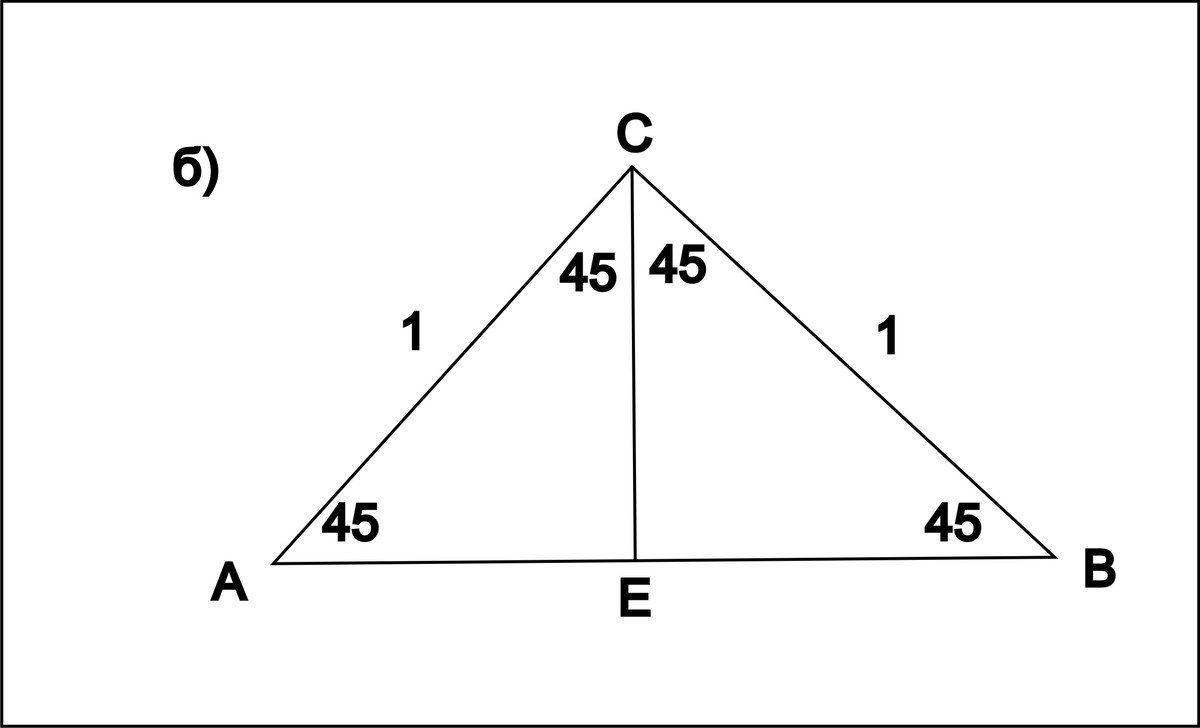
АС=СВ треугольник равнобедренный
АЕ=АВ/2
CE²=AC²-AE²
CE=(√2)/2
S(ABC)=(1/2)·AB·CE=(1/2)·√2·(√2)/2=1/2
АВ=√((хb-xa)²+(yb-ya)²+(zb-za)²)
а)AB=√((-1-4)²+(2+1)²+(4-2)²)
AB=√(25+9+4)=√38
BC=√((2+1)²+(4-2)²+(-1-4)²)=√(9+4+25)=√38
AC=√((2-4)²+(4+1)²+(-1-2)²=√(4+25+9)=√38
AB=BC=AC
треугольник равносторонний все углы 60
высота треугольника Н=АВ·сos30=√38·((√3)/2)=(√114)/2
S(ABC)=H·AC·(1/2)=((√114)/2)·√38·(1/2)=(19√3)/2
б)АВ=√(0+(2-1)²+(1-2)²=√2
АС=√(0+(2-1)²+0)=1
СВ=√(0+0+(1-2)²)=1
АС=СВ треугольник равнобедренный
АЕ=АВ/2
CE²=AC²-AE²
CE=(√2)/2
S(ABC)=(1/2)·AB·CE=(1/2)·√2·(√2)/2=1/2
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: мам2016
Предмет: Английский язык,
автор: veronadz
Предмет: Английский язык,
автор: Viciняня
Предмет: Алгебра,
автор: nattttt
Предмет: Литература,
автор: madinkamadinka88