Question

Даю 63 балла. Постройте график функции y=(х^2-x-6)*(x^2-x-2) / х^2-4; При каких значениях m прямая y=m имеет с графиком ровно одну общую точку

Answer 1

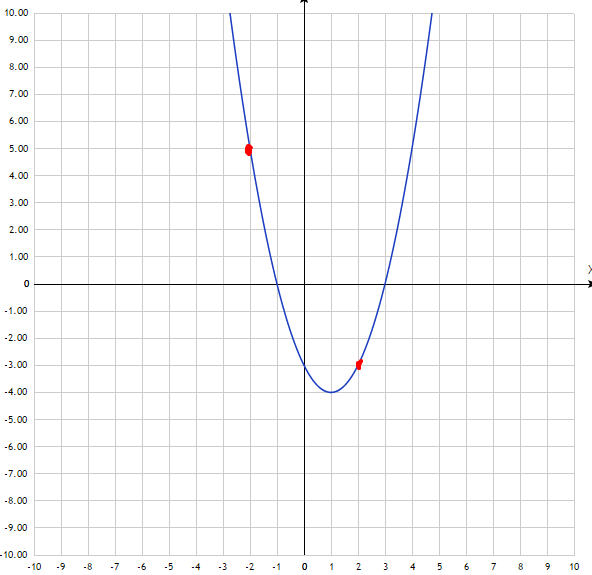
преобразуем выражение в $\frac{(x-3)(x-2)(x+2)(x+1)}{(x+2)(x-2)}$ сокращаем ,но помним, что x не равен +-2. Получили (x-3)(x+1). график прикрепил, красные точки выколотые y=m -горизонтальная прямая на уровне m. из графика видим, 1 точка будет в вершине и на уровне выколотых точек. ищем y вершины. х вершины по формуле -b/2a, график имеет формулу x^2-2x-3, b=-2, a=1, x вершины=1, подставим 1 в уравнение, получим -4, это у, прим m=-4 1 общая точка. теперь выколотые рассмотрим, подставим в уравнение +-2, получим -3 и 5 соответственно
При m=-4, -3, 5 одна общая точка

Answer 2

Да тут всё легко:
1)Раскладываешь каждый трехчлен на множители
$x^2-x-6=(x-x_1)(x-x_2)$$x^2-x-6=0; D=1-4*(-6)=5^2; x= \frac{1б5}{2}; x=-2; x=3;$ $x^2-x-6=(x-3)(x+2)$;
$x^2-x-2=0; D=1-4*(-2)=3^2; x= \frac{1б3}{2}; x=2; x=-1;$ $x^2-x-2=(x-2)(x+1)$
2)В знаменателе $x^2-4=(x-2)(x+2)$
3)Собираем всё в кучу, сокращаем, не забывая о нулях в знаменатале 2 и -2 (точки будут выколотыми) $\frac{(x-3)(x+2)(x-2)(x+1)}{(x-2)(x+2)}=(x-3)(x+1); x \neq б2$
4) А дальше строим обычную параболу $y=x^2-2x-3; x_0=- \frac{b}{2a}=- \frac{-2}{2}=1; y_0=1^2-2*1-3=-4 ;(1;-4)$
По разложению первоначальному нули функции есть : -1 и 3 (при них y=0), это точки пересечения графика с осью OX, с осью OY : $0^2-2*0-3=-3; (0;-3)$, можно ещё взять дополнительные точки (не обязательно)
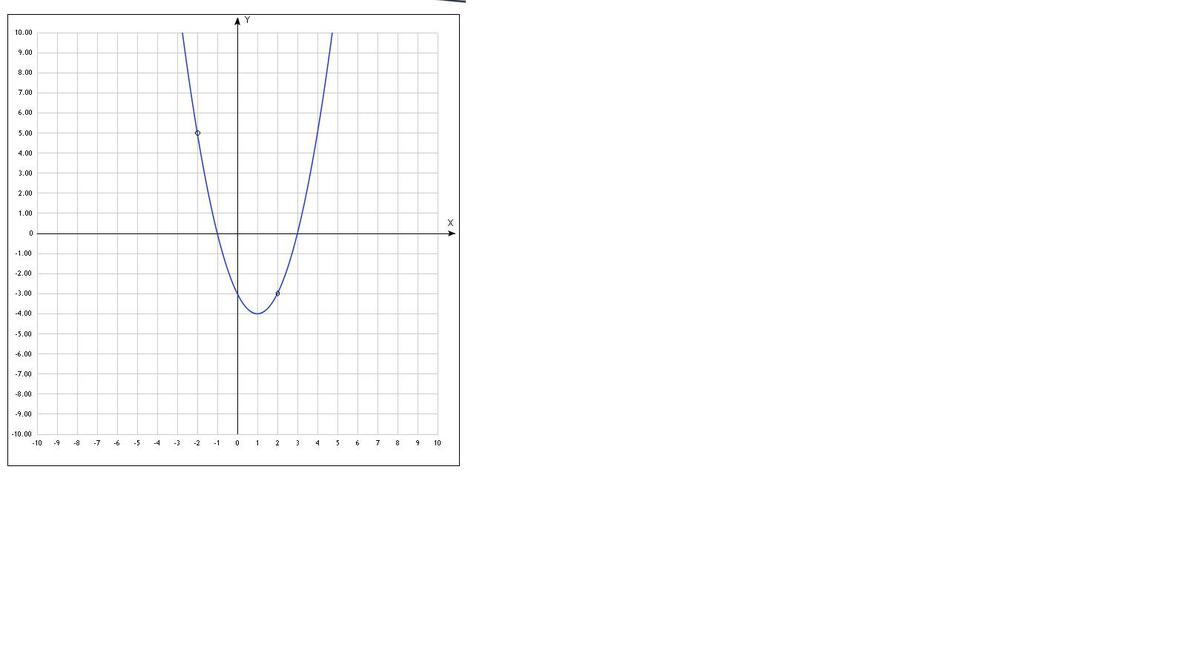
График в файле. Так как есть точки выколотые, то при них тоже будет 1 общая точка и при вершине параболы. То есть $m=-4; m=-3; m=5.$
Ответ: -4, -3, 5.