Предмет: Геометрия,
автор: marinka31
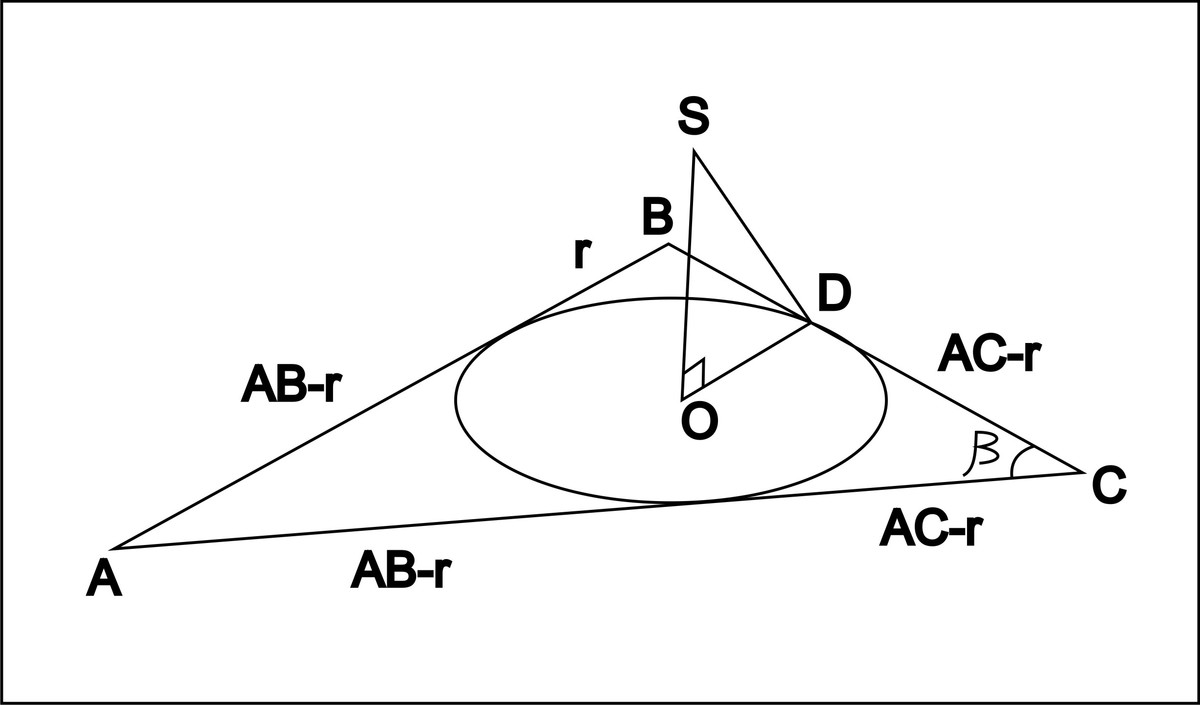
Из центра О ,вписанной в прямоугольный треугольник АВС окружности,проведен перпендикуляр OS до плоскости АВС,найти расстояние от точки S до катета ВС,ЕСЛИ АС=6,угол С=β,а длина перпендикуляра равна радиусу вписанной окружности.
Ответы
Автор ответа:
2
радиус вписанной в угол окружности отсекает от его сторон одинаковые отрезки
АС=АВ-r+BC-r
r=(AB+BC-AC)/2
AB=AC·sinβ
BC=AC·cosβ
r=(AC·cosβ+AC·sinβ-AC)/2=(AC(cosβ+sinβ-1))/2
OD=r
SD²=SO²+OD²=2r²
SD=√2r
SD=(6√2(cosβ+sinβ-1))/2=3√2(cosβ+sinβ-1)
АС=АВ-r+BC-r
r=(AB+BC-AC)/2
AB=AC·sinβ
BC=AC·cosβ
r=(AC·cosβ+AC·sinβ-AC)/2=(AC(cosβ+sinβ-1))/2
OD=r
SD²=SO²+OD²=2r²
SD=√2r
SD=(6√2(cosβ+sinβ-1))/2=3√2(cosβ+sinβ-1)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: olyavolnyh991
Предмет: Русский язык,
автор: Mair666
Предмет: Русский язык,
автор: Menshchikova19
Предмет: Алгебра,
автор: Аноним