Question

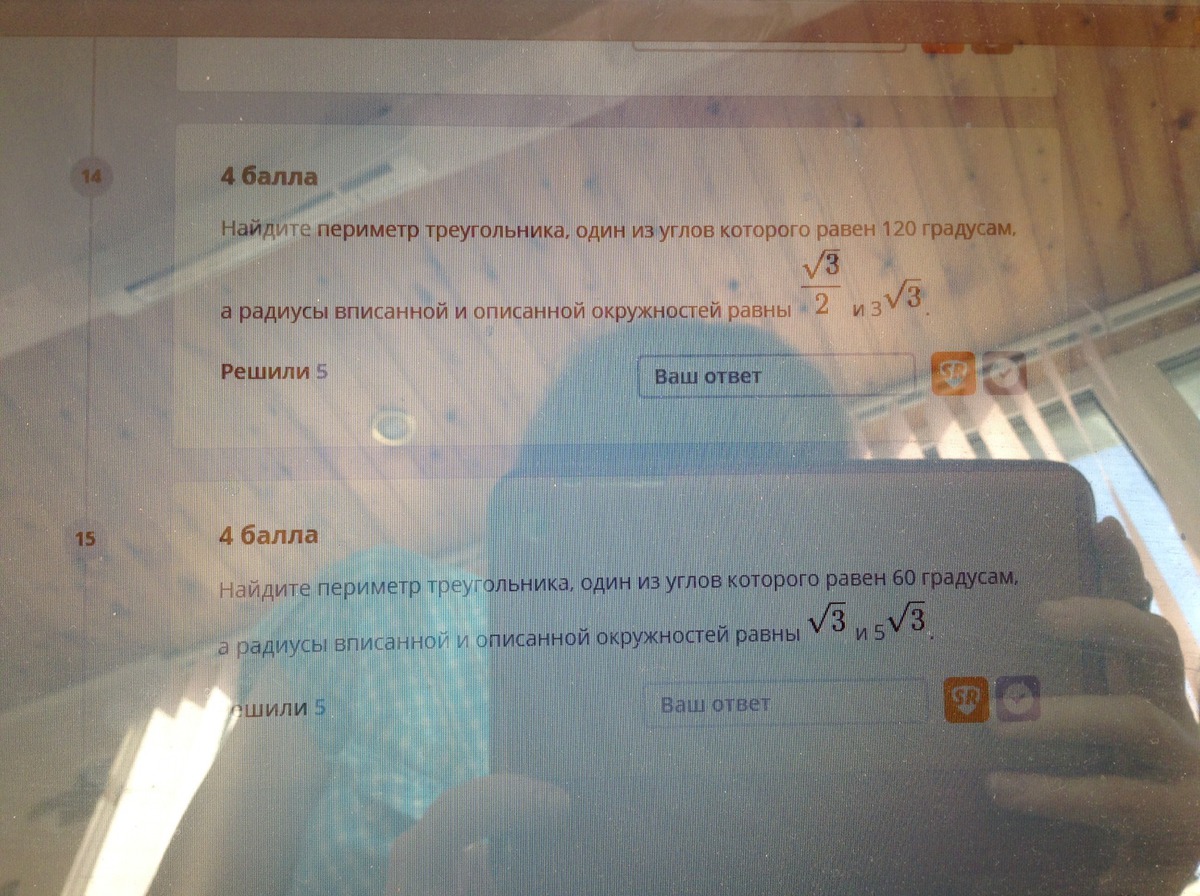
100 баллов . СЛОЖНАЯ ГЕОМЕТРИЯ
2 аналогичные задачи
Нужны точные ответы!!!

Answer 1

14)  c/sinC =2R ⇒c =2R*sin120° =2*3√3*√3/2 = 9;
c² =a² +b² -2ab*cos120° =a² +b² +ab    (1)
S =(a+b+c)/2 *r ;
1/2ab*sin120° =(a+b+9)/2*√3/2
 √3/4 ab =(a+b+9)*3/4 ;
ab =a+b+9       (2)
------------------------------
{ a² +b² +ab =81; ab =a+b+9 .{ (a +b)² - ab =81; ab =a+b+9 .
⇔{(a+b)² -(a+b+9) =81 ; ab =a+b+9.
(a+b)² -(a+b) -90 =0 ;
a+b =10      ;                ***    a+b= -9*** =
P =a+b+c  =10+9 =19 .

аналогично    вторая:
15) c/sinC =2R ⇒c =2R*sin60° =2*5√3*√3/2 = 15;
c² =a² +b² -2ab*cos60° =a² +b² - ab    (1)
S =(a+b+c)/2 *r ;
1/2ab*sin60° =(a+b+15)/2*√3 ;
 √3/4 ab =(a+b+15)*√3/2 ;
ab =2(a+b)+30                                       (2)
------------------------------------------------------------------------------------------
{ a² +b² +ab =225 ; ab =2(a+b)+30 .{ (a +b)² - 3ab =225 ; ab =2(a+b)+30 .
⇔{(a+b)² -6(a+b) -90 =225 ;  ab =2(a+b)+30.
(a+b)² -6(a+b) -315=0 ;

a+b =21     ;                ***    a+b= -15***=
P = (a+b)+c  =21+15=36.

Answer 2

Треугольник ABC, угол A равен α; радиусы вписанной и описанной окружности r и R. Как обычно, напротив угла лежит одноименная сторона, только обозначенная маленькой букой (то есть BC = a; AB = c; AC = B);
Пусть стороны касаются вписанной окружности в точках M (BC), N (AC), K (AB). Я обозначаю x = AK = AN; y = BK = BM; z = CM = CN;
x + y = c;
x + z = b;
y + z = a;
Откуда x - y = b - a; 2*x = c + b - a; x = (c + b - a)/2 = p - a;
где p = (a + b + c)/2; ПОЛУпериметр треугольника ABC;
Далее все очевидно (O - центр вписанной окружности).
Из треугольника AOK;
x = r*ctg(α/2);
по теореме синусов
a = 2*R*sin(α);
Откуда
p - 2*R*sin(α) = r*ctg(α/2); само собой, периметр равен 2*p;
2*p = 4*R*sin(α) + 2*r*ctg(α/2);
1) α = 120°; sin(α) = √3/2; ctg(α/2) = 1/√3; R = 3√3; r = √3/2;
2*p = 19;
2) α = 60°; sin(α) = √3/2; ctg(α/2) = √3; R = 5√3; r = √3;
2*p = 36;