Question

100 баллов !СЛОЖНАЯ ГЕОМЕТРИЯ
Нужны точные ответы! (С понятным решением, если можно)
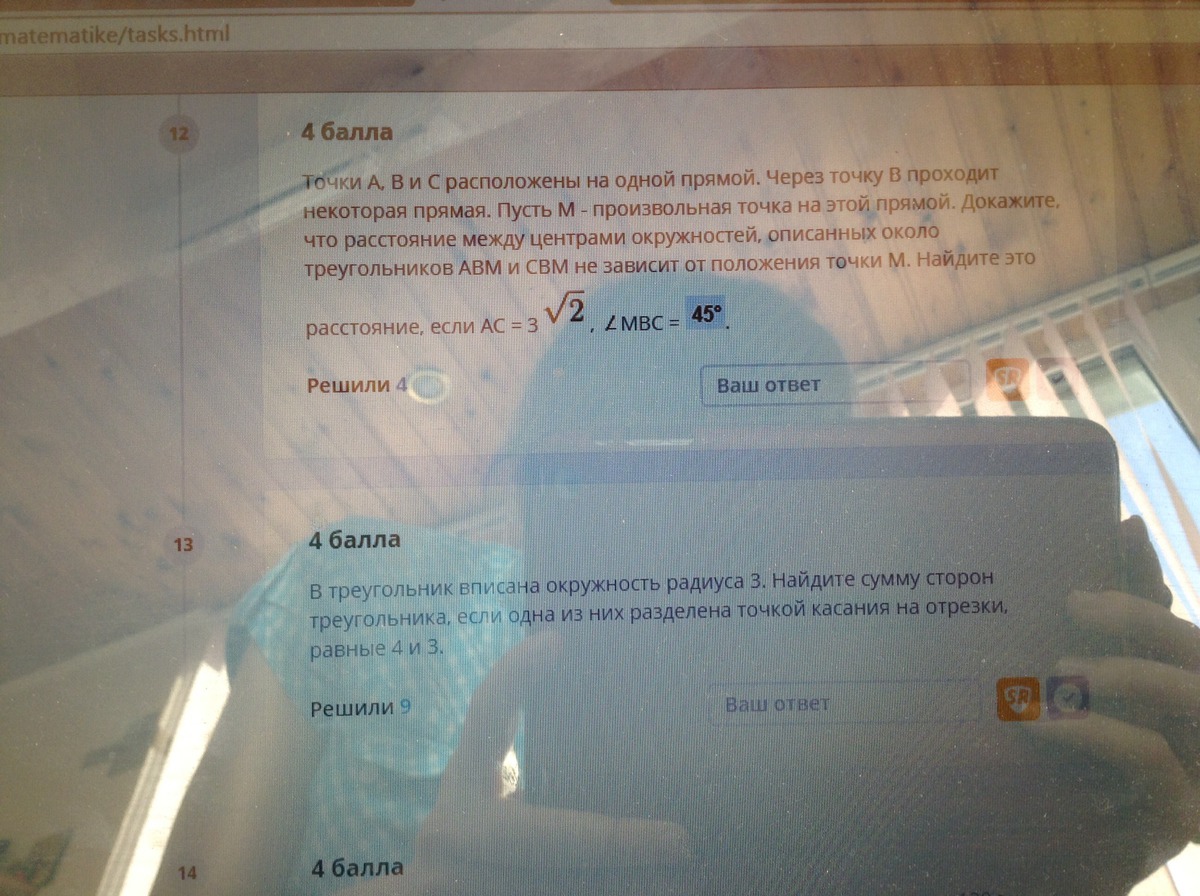
12,13

Answer 1

12)
Пусть есть окружность, проходящая через 3 точки - начало координат M (0,0), точку на оси ординат N (0, 2*n) и точку A с координатами (a*cos(α), a*sin(α));
Центр окружности лежит где то на прямой y = n; пусть это точка с координатами (c, n);
Тогда
(x - c)^2 + (y - n)^2 = R^2;
c^2 + n^2 = R^2;
и, кроме того, уравнению окружности удовлетворяет точка A.
x^2 - 2*x*c + y^2 - 2*y*n = 0; (R^2 благополучно сократился);
a^2*(cos(α))^2 - 2*a*cos(α)*c + a^2*(sin(α))^2 - 2*a*sin(α)*n = 0;
с = a/(2*cos(α)) - n*tg(α);
Это все, что нужно для решения задачи.
Пусть есть другая точка B с координатами (b*cos(α), b*sin(α)); эта точка лежит на той же прямой MA, или на её продолжении за точку М, если b - отрицательно.
Тогда центр окружности, проходящей через точки M(0,0) N(0,2*n) и B имеет координаты (c', n) где
c' = b/(2*cos(α)) - n*tg(α);
расстояние между центрами равно
lc - c'l = la - bl/(2*cos(α)) = AB/(2*cos(α));
где AB - расстояние между A и B.
Разумеется, эта величина не зависит от n;
Если подставить численные значения, то ответ будет 3;
ошибка в комментариях связана с тем, что я искал расстояния между точками пересечения окружностей с "осью X", координаты этой точки (2*c,0). Уж простите.
13) По формуле Герона
r^2 = (p - a)*(p - b)*(p - c)/p; р - ПОЛУпериметр.
в данном случае r = 3; c = 7;
9*p = (p - 7)*3*4; p = 28;
сумма сторон равна 2*p = 56;