Question

Ау,старшеклассники!!!11-классники!!!Немножко нужна помощь ваша в виду объяснения применения арккосинуса и как -что через него выражается.Решение вот.С меня лучший ответ.
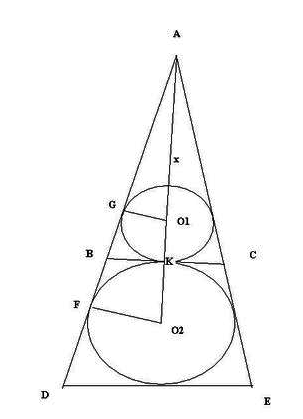
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.

Answer 1

  arccosa это  просто угол в градусах   
 
То есть вы хотите узнать как получилось 
  $sin(arccos(-\frac{1}{63})-\frac{\pi}{2}) = sin(arccos(-\frac{1}{63}))*cos\frac{\pi}{2}-\\ cos(-arccos(- \frac{1}{63}))*sin\frac{\pi}{2} \\ arccos(-\frac{1}{63})=arcsin\sqrt{1-\frac{1}{63^2}} = arcsin\sqrt{\frac{ 3968}{63^2}}\\ sin(arcsina)=a\\ cos(arccosa)=a\\\\ sin(arccos(-\frac{1}{63})-\frac{\pi}{2}) =\frac{1}{63}*1$ 
 его двойной угол тогда 
 $sin2a=2sina*cosa=2*\frac{1}{63}*\sqrt{1-\frac{1}{63^2} } = \frac{ 2*\sqrt{3968}}{3969}$