Предмет: Геометрия,
автор: Lerka35152
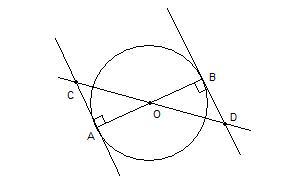
Отрезок AB является диаметром окружности с центром в точке О. В точках А и В проведены касательные к окружности. Через центр окружности проведена прямая, которая пересекает касательные в точках C и D. Докажите, что длины отрезков OC и OD равны.
Заранее огромное спасибо♥
Ответы
Автор ответа:
3
Поскольку касательные перпендикулярны радиусу в точке касания, то треугольники ОАС и OBD прямоугольные. Рассмотрим их. Здесь:
- АО=ВО как радиусы окружности;
- <COA=<DOB как вертикальные углы.
Используем один из признаков равенства прямоугольных треугольников: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны. Значит, в равных треугольниках ОАС и OBD равны и их гипотенузы. ОС=OD.
- АО=ВО как радиусы окружности;
- <COA=<DOB как вертикальные углы.
Используем один из признаков равенства прямоугольных треугольников: если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны. Значит, в равных треугольниках ОАС и OBD равны и их гипотенузы. ОС=OD.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: oksanaoleshko
Предмет: Русский язык,
автор: vanyushamoisee
Предмет: Английский язык,
автор: boanosje
Предмет: Математика,
автор: pomogately
Предмет: Алгебра,
автор: kubanychbekovadjamil