Предмет: Геометрия,
автор: MaxGol
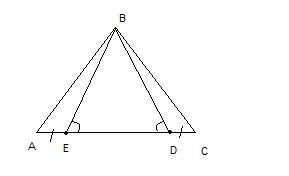
На стороне AC треугольника ABC выбраны точки D и E так что углы ADB и BEC равны.оказалось что отрезки AE и CD тоже равны.докажите что треугольник ABC - равнобедренный
Ответы
Автор ответа:
26
Рассмотрим треугольник EBD. Углы при его основании ED равны по условию, значит он равнобедренный, и ВЕ=BD.
Рассмотрим треугольники АЕВ и CDВ. Здесь:
- АЕ=CD по условию;
- ВЕ=BD как доказано выше;
- <AEB=180-<BEC, <CDB=180-<ADB. Но <BEC=<ADB по условию, значит <AEB=<CDB.
Следовательно, треугольники АЕВ и CDВ равны по двум сторонам и углу между ними (первый признак равенства треугольников), и АВ=СВ, т.е. треугольник АВС - равнобедренный.
Рассмотрим треугольники АЕВ и CDВ. Здесь:
- АЕ=CD по условию;
- ВЕ=BD как доказано выше;
- <AEB=180-<BEC, <CDB=180-<ADB. Но <BEC=<ADB по условию, значит <AEB=<CDB.
Следовательно, треугольники АЕВ и CDВ равны по двум сторонам и углу между ними (первый признак равенства треугольников), и АВ=СВ, т.е. треугольник АВС - равнобедренный.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Savostyanova3
Предмет: Английский язык,
автор: magnat4444
Предмет: Русский язык,
автор: LinKaBrain
Предмет: Алгебра,
автор: commu2005
Предмет: Литература,
автор: Аноним