Предмет: Геометрия,
автор: 79092971981
В треугольник ABC, в котором LA = 90°, вписана окружность с центром О. Найдите отрезки, на которые точка касания этой окружности и прямой АС делит сторону АС, если ОС = 5 дм и АО = = 3^2 дм.
Ответы
Автор ответа:
5
Найти: АК, КС.
Красным цветов выделены дополнительные построения - радиусы, проведенные в т. касания. ОМ=ОR=OK=R
AMOK - квадрат, т.к. МО=ОК (признак квадрата) => MO=OK=MA=AK
Из прямоуг. ΔAMO по т. Пифагора:
АО²=АМ²+МО²
18=2МO²
MO²=9
MO=3 ⇒ AK=3
Из прямоугольного ΔСOK по т. Пифагора:
СО²=ОК²+КС²
25=9+КС²
КС²=16
КС=4
Красным цветов выделены дополнительные построения - радиусы, проведенные в т. касания. ОМ=ОR=OK=R
AMOK - квадрат, т.к. МО=ОК (признак квадрата) => MO=OK=MA=AK
Из прямоуг. ΔAMO по т. Пифагора:
АО²=АМ²+МО²
18=2МO²
MO²=9
MO=3 ⇒ AK=3
Из прямоугольного ΔСOK по т. Пифагора:
СО²=ОК²+КС²
25=9+КС²
КС²=16
КС=4
Приложения:
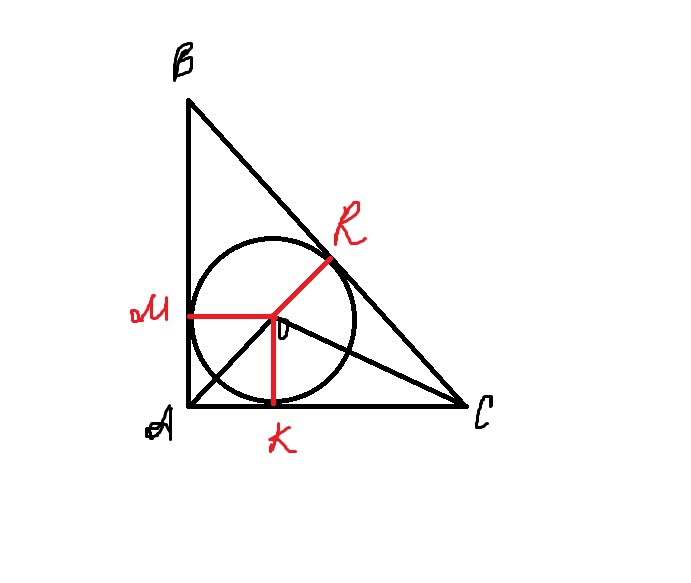
Ходок1:
AO^2=81
Похожие вопросы
Предмет: Русский язык,
автор: roksi100200
Предмет: Английский язык,
автор: s45567231
Предмет: Русский язык,
автор: marina739854p128q5
Предмет: Русский язык,
автор: anahit598