Предмет: Геометрия,
автор: homkadron18
ПОМОГАЙТЕ, К ЕГЭ ГОТОВЛЮСЬ
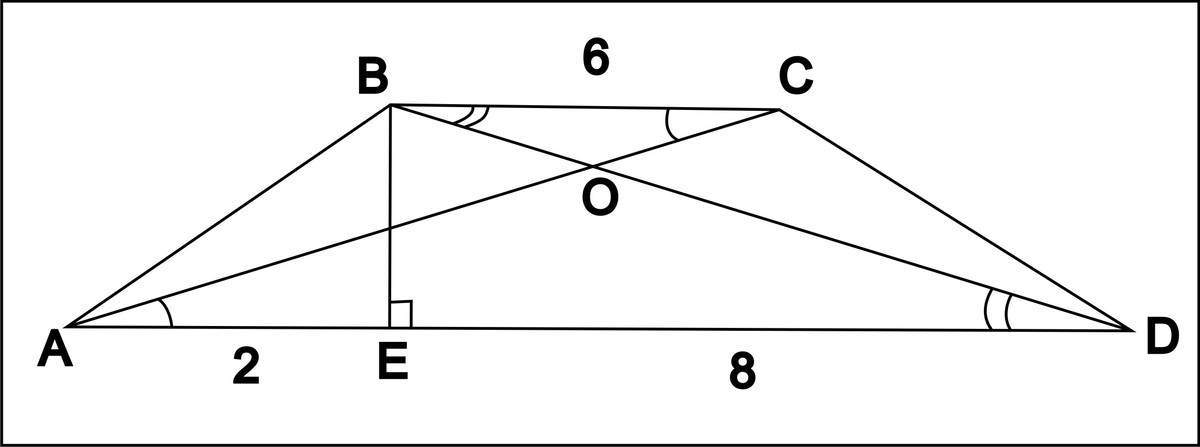
В равнобедренной трапеции ABCD основания AD и ВС равны соответственно 10 см и 6 см, угол А равен 30°. а) Докажите подобие треугольников AOD и BOC и
найдите отношение их площадей, если О - точка пересечения диагоналей трапеции. б) Найдите радиус описанной около трапеции окружности.
Ответы
Автор ответа:
3
а)угол ВСО= углу ОАD как накрест лежащие при параллельных ВС и AD
угол СВО=углу ODA как накрест лежащие при параллельных BC и AD
угол ВОС=углу AOD как вертикальные
получается в треугольниках ВСО и AOD соответсвенные углы равны
=>треугольники подобны
AD/BC=10/6=5/3=k-коэффициент подобия треугольников
площади треугольников относятся как коэффициент подобия в квадрате
k²=25/9
S(AOD)/S(BOC)=25/9
б)tg30=BE/AE
BE/2=1/√3
BE=2/√3
BD²=ED²+BE²
BD²=64+4/3
BD=14/√3
R=BD/(2sinBAD)=BD/(2sin30)=14/√3
угол СВО=углу ODA как накрест лежащие при параллельных BC и AD
угол ВОС=углу AOD как вертикальные
получается в треугольниках ВСО и AOD соответсвенные углы равны
=>треугольники подобны
AD/BC=10/6=5/3=k-коэффициент подобия треугольников
площади треугольников относятся как коэффициент подобия в квадрате
k²=25/9
S(AOD)/S(BOC)=25/9
б)tg30=BE/AE
BE/2=1/√3
BE=2/√3
BD²=ED²+BE²
BD²=64+4/3
BD=14/√3
R=BD/(2sinBAD)=BD/(2sin30)=14/√3
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Jånę
Предмет: Українська мова,
автор: Lizamog1
Предмет: Русский язык,
автор: бекзод3344
Предмет: Литература,
автор: ВасяПупин
Предмет: Литература,
автор: Аноним