Предмет: Математика,
автор: Ленгит
В некотором треугольнике медиана,
биссектриса и высота, проведенные из одной вершины, делят этот угол на четыре равные части. Найдите углы этого треугольника.
Ответы
Автор ответа:
6
Пусть D - точка пересечения биссектрисы с описанной вокруг треугольника окружностью. GD || BF, то есть угол FBD = углу BDE = α. Значит BE=ED и BG=GD (как радиусы описанной окружности). Отсюда угол DBG = углу DBE. В свою очередь это означает, что точка G и E совпадают, значит AC - диаметр описанной окружности. Вписанный угол, который опирается на диаметр равен 90 градусов. Следовательно α=22,5, угол ACB = 90, угол ABC = 22.5, а угол BAC = 90 - 22.5 = 67.5
Приложения:
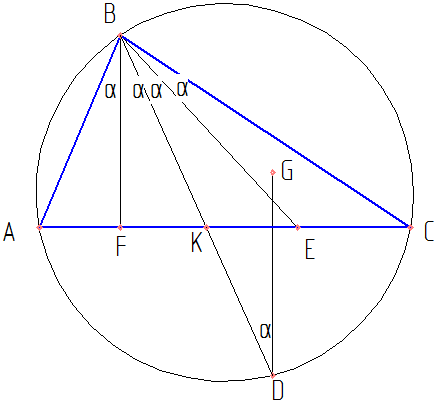
uhbifkov:
ща перепроверил,немного изменил,так что просмотри ещё раз буквы
Похожие вопросы
Предмет: Қазақ тiлi,
автор: akerkeusaeva20jejdjd
Предмет: Другие предметы,
автор: бро120
Предмет: Русский язык,
автор: FACE111111111111
Предмет: Английский язык,
автор: koceno4ek
Предмет: Биология,
автор: s242ss