Предмет: Геометрия,
автор: efromeevdaniil
радиус окружности с центром O равен 4 найдите длину хорды BC, если косинус BOC равен 7/8.
Ответы
Автор ответа:
0
1).
По т. косинусов ВС ²=ОС²+ОВ² - 2*ОС*ВС*cos BOCВС²=16+16-32*7/8ВС²=4
ВС=√4=2
-------
2).
Сделаем рисунок.
Опустим из С перпендикуляр СА на радиус ОВ.
В прямоугольном треугольнике АОС косинус АОС=АО/СО=7/8
Пусть коэффициент этого отношения будет х.
Тогда СО=8х=4⇒
х=4:8=0,5
ОА=7х=3,5
ВА=4-3,5=0,5
СА²=(СО²- АО²)=3,75
ВС²=СА²+ВА²=3,75+0,25=4
ВС=√4=2
По т. косинусов ВС ²=ОС²+ОВ² - 2*ОС*ВС*cos BOCВС²=16+16-32*7/8ВС²=4
ВС=√4=2
-------
2).
Сделаем рисунок.
Опустим из С перпендикуляр СА на радиус ОВ.
В прямоугольном треугольнике АОС косинус АОС=АО/СО=7/8
Пусть коэффициент этого отношения будет х.
Тогда СО=8х=4⇒
х=4:8=0,5
ОА=7х=3,5
ВА=4-3,5=0,5
СА²=(СО²- АО²)=3,75
ВС²=СА²+ВА²=3,75+0,25=4
ВС=√4=2
Приложения:
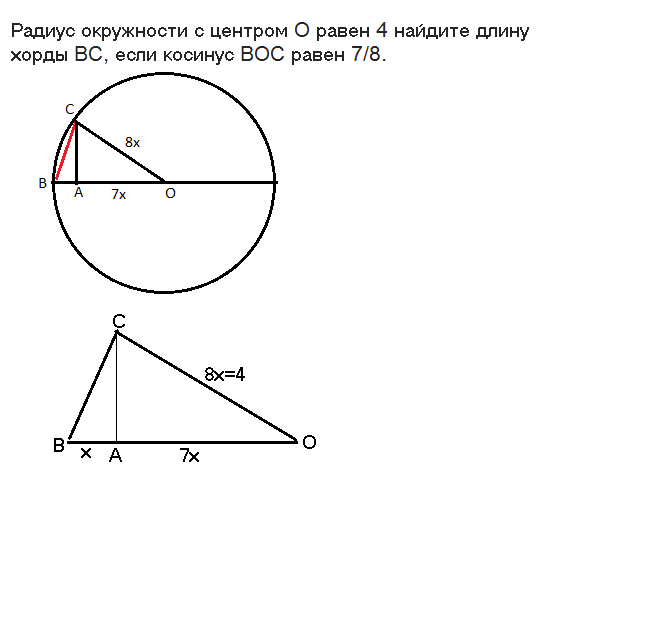
Похожие вопросы
Предмет: Английский язык,
автор: Evgesha0me
Предмет: Окружающий мир,
автор: MaryIvanova228
Предмет: Окружающий мир,
автор: накнак1
Предмет: Математика,
автор: sasha971172
Предмет: Алгебра,
автор: larex6202