Question

найдите площадь трапеции диагонали которой равны 10 и 8 а средняя линия равна 3

Answer 1

Ответ:

Площадь трапеции равна 24 кв.ед.

Объяснение:

Пусть дана трапеция АВСD.

Диагонали трапеции АС =10 ед. , ВD= 8 ед.

Средняя линия равна 3 ед.

Средняя линия равна полусумме оснований. Значит, сумма оснований

ВС+АD =6.

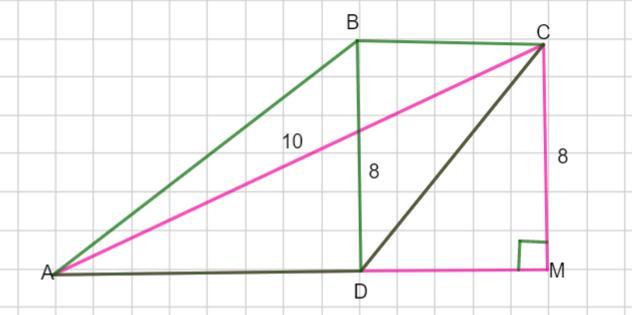
Выполним дополнительное построение. По строим СМ ║ ВD.

Тогда четырехугольник ВСМD - параллелограмм. В параллелограмме противолежащие стороны равны.

Значит,

CM= BD = 8 ед. , DM= BC

Тогда сумма сторон будет

DM+АD = 6  Отсюда  АМ =6 ед.

Рассмотрим Δ АСМ. Так как

$AC^{2} =CM^{2} +AM ^{2} ;\\10^{2} =8^{2} +6^{2} ;\\10=64+36;\\100=100$

То по теореме, обратной теореме  Пифагора, Δ АСМ - прямоугольный с гипотенузой АС.

Теорема, обратная теореме Пифагора: если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный.

Тогда высота трапеции будет диагональ BD.

Так как СМ ⊥ АМ, то BD⊥ АМ.

Рисунок получится во вложении.

Площадь трапеции равна произведению средней линии трапеции на высоту трапеции.

Значит,

$S= 3\cdot8 =24$  кв. ед.