Question

найти точки экстремума функции f(x)=0.5x^4-2x^3

Answer 1

Находим f`(x).
f`(x)=(0,5x⁴-2x³)`=0,5·4x³-2·3x²=2x³-6x²=2x²(x-3)
f`(x)=0
2x²(x-3)=0
x=0  x-3=0 - точки возможного экстремума.
Применяем достаточное условие экстремума и находим знак производной
__-____(0)__-____(3)___+__

х=3 - точка минимума, производная меняет знак с - на +.
х=0 - точкой экстремума не является.
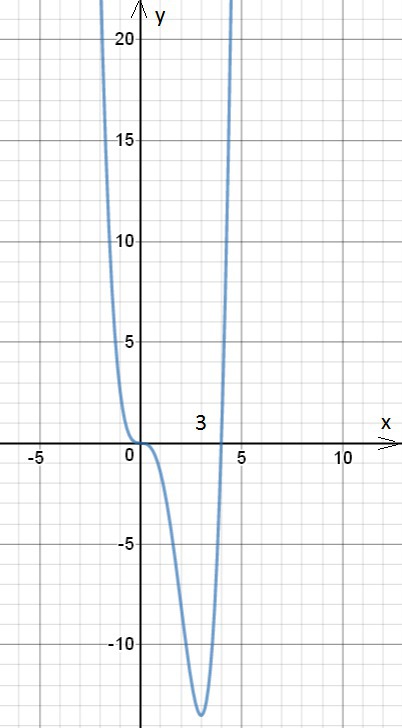
См. график функции в приложении.