Question

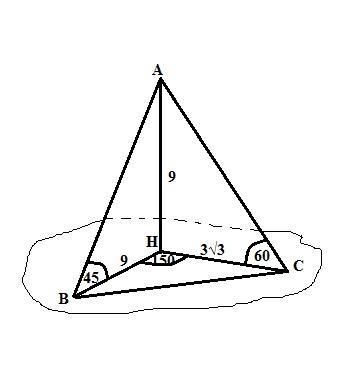
Точка A находится на расстоянии 9 см от плоскости a . Наклонные AB и AC образуется с плоскостью a углы 45 градусов и 60 градусов. Найти расстояние между точками B и C, если угол между проекциями наклонных равен 150 градусов

Answer 1

Ответ:

ВС = 3√21 см.

Объяснение:

Пусть основание перпендикуляра, опущенного на плоскость α - точка Н.

AH=9 см,<ABH=45°,<ACH=60°,<BHC=150°.

Заметим, что Cos150° = Cos(180 - 30) = -Cos30° = - √3/2.

В прямоугольном треугольнике АВН острые углы равны по 45°, треугольник равнобедренный и ВН=АН= 9см.

В прямоугольном треугольнике АСН тангенс угла С равен

Tg60 = √3 = AH/CH  => CH = 9/√3 = 3√3 см.

В треугольнике ВНС по теореме косинусов:

BC²=BH²+CH²-2*BН*CH*cos150 = 81+27 - 2*9*3√3*(-√3/2) или

ВС² = 108+81 =189

BC = √189 = 3√21 см.