Предмет: Алгебра,
автор: sanzhar999
f(x)=(lnx)^x
f'(e)=?
Приложения:
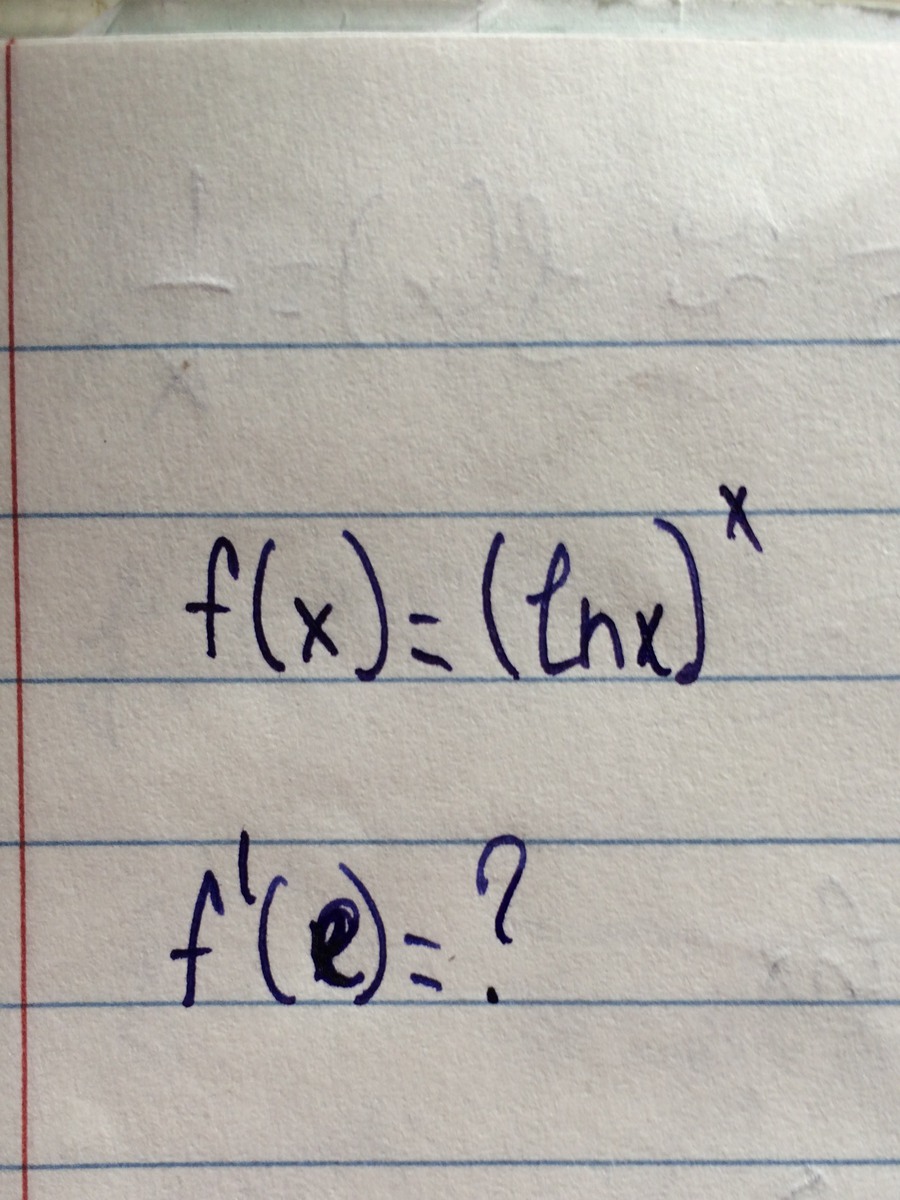
Ответы
Автор ответа:
2
sanzhar999:
здесь не до конца
Я добавила уже давно
приложение тупануло вроде. поверх комментов решение написано
Ну, это не моя вина... y'(e)=1
Похожие вопросы
Предмет: Русский язык,
автор: nonoonono
Предмет: Другие предметы,
автор: dimaddv13
Предмет: Русский язык,
автор: 998800
Предмет: Алгебра,
автор: misha2904