Предмет: Геометрия,
автор: EwgeneWald
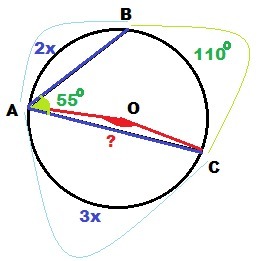
Точки А, В, С лежат на окружности с центром в точке О. Дуга АВ относится к дуге АС как 2:3. Дуга АВ<180°, дуга АС<180°, угол ВАС=55°. Чему равен угол АОС?
Ответы
Автор ответа:
30
∪AB / ∪AC = 2/3 ⇒ ∪AC = 3∪AB/2 = 1,5∪AB
∠BAC = 55° - вписанный угол равен половине дуги, на которую опирается
⇒ ∪BC = 2*∠BAC = 2*55° = 110°
Дуги AB, AC и BC образуют окружность, значит, в сумме дают 360°
∪AB + ∪AC + ∪BC = 360°
∪AB + 1,5∪AB + 110° = 360°
2,5∪AB = 250°
∪AB = 100°
∪AC = 1,5∪AB = 1,5 * 100° = 150°
∠AOC - центральный, равен дуге, на которую опирается. ⇒
∠AOC = ∪AC = 150°
Ответ: ∠AOC = 150°
∠BAC = 55° - вписанный угол равен половине дуги, на которую опирается
⇒ ∪BC = 2*∠BAC = 2*55° = 110°
Дуги AB, AC и BC образуют окружность, значит, в сумме дают 360°
∪AB + ∪AC + ∪BC = 360°
∪AB + 1,5∪AB + 110° = 360°
2,5∪AB = 250°
∪AB = 100°
∪AC = 1,5∪AB = 1,5 * 100° = 150°
∠AOC - центральный, равен дуге, на которую опирается. ⇒
∠AOC = ∪AC = 150°
Ответ: ∠AOC = 150°
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: lerabikir
Предмет: Английский язык,
автор: Yasmin2121
Предмет: Окружающий мир,
автор: You2038Problem2038
Предмет: Английский язык,
автор: sergienko2017