Question

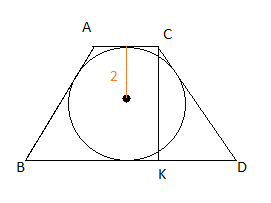
В равнобокую трапецию площадью 20 см2 вписано окружность радиусом 2 см. Найдите стороны трапеции.

Answer 1

СК = 2r = 2*2 = 4см.

Выразим сумму оснований через площадь
$S= \frac{AC+BD}{2}\cdot CK \\ AC+BD= \frac{2S}{CK} = \frac{2\cdot 20}{4}=10$

По свойству радиусу вписанной окружности
AB + CD = AC+BD
Боковые стороны АВ и СД равны
2AB=AC+BD
2AB = 10
AB= 5см

И так две стороны нашли, найдем основания

С треугольника CKD (<CKD = 90)

$KD= \sqrt{CD^2-CK^2}=3$ см

$BC= \frac{P-2AB-2CK}{KD}$

$P= \frac{2S}{CK} +2AB= \frac{2\cdot 20}{4}+2\cdot 5=20$см

Откуда ВС

$BC= \frac{20-2\cdot 5-2\cdot 3}{2}=2$ см

AD = 10-BC=10-2= 8 см

Ответ: 2см; 8см; 5см; 5см.

Answer 2

Нам дан радиус вписанной окружности.
$r=2$
Следовательно h=2r=4.

$S=l*h \\ 20=l*4\\ l=5$
Нашли среднюю линию трапеции.

$l=\frac{a+b}{2}\\ 5=\frac{a+b}{2} \\ a+b=10$

Нашли сумму оснований.
Если окружность вписана в трапецию, значит сумма оснований и боковых сторон равна. А так как трапеция равнобокая, то боковые стороны равны.
c - боковые стороны.
$a+b=2c\\ 10=2c\\ c=5$

Дальше находим по Т. Пифагора.
$KD=\sqrt{25-16}=\sqrt9=3$

АК по свойству равнобокой трапеции равен средней линии.
AK=5
AC=5+3=8

8+b=10
b=2

Ответ: 10, 2, 10, 8