Предмет: Алгебра,
автор: bentos
5cos²x+7cosx-6=0
8cos²x-10sinx-11=0
Криблекраблебумс:
ммм... какие классные примеры
да...
реально. офигенные. кайфец их решать
жаль, что мне нужно свои решать. скучные
что ты делаешь, человек?)
реально не могу решить, очень очень нужно
первое методом замены. второе раскрыть по тригонометрическому тождеству и потом опять-таки методом замены
спасибо)
Ответы
Автор ответа:
3
Автор ответа:
2
Решение во вложении...........
Приложения:
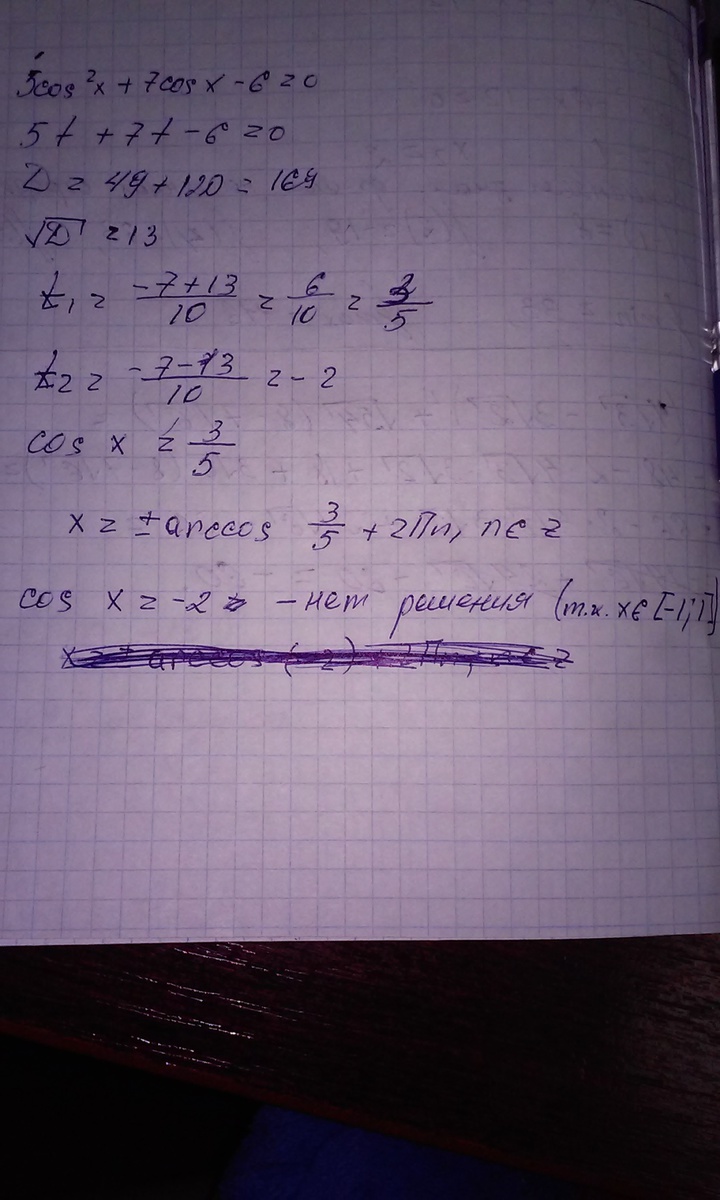

Похожие вопросы
Предмет: Окружающий мир,
автор: мася2314
Предмет: Қазақ тiлi,
автор: Камиль877784612008
Предмет: Другие предметы,
автор: ОмскийШкет
Предмет: Математика,
автор: alekseytognevoy