Предмет: Алгебра,
автор: NichaKatya
помогите пожалуйста решить
Приложения:
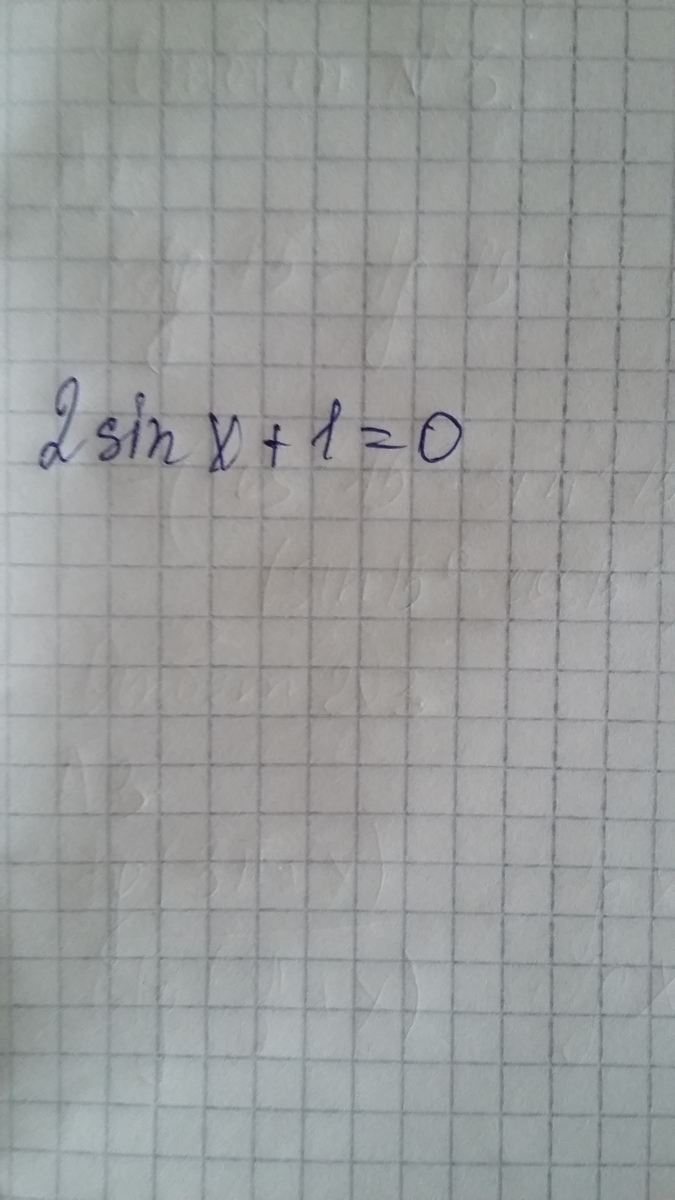
Ответы
Автор ответа:
1
По формуле общего вида.
А вот другие два решения:
Freakazoid:
Это по формуле общего вида, но если надо другие решения, могу и их написать
если решение правильное и устраивает вас - отмечайте как "лучшее решение", за это даются вам баллы.
Автор ответа:
0
2sinx + 1 =0
sin x = -0.5
x=
sin x = -0.5
x=
Похожие вопросы
Предмет: Русский язык,
автор: Фатя11111111
Предмет: Русский язык,
автор: Polina150605
Предмет: Русский язык,
автор: vladvladoskar
Предмет: Математика,
автор: leylaaliyeva34
Предмет: Математика,
автор: OnnySay18