Предмет: Алгебра,
автор: Lidanext
срочно,докажите тождество
Приложения:
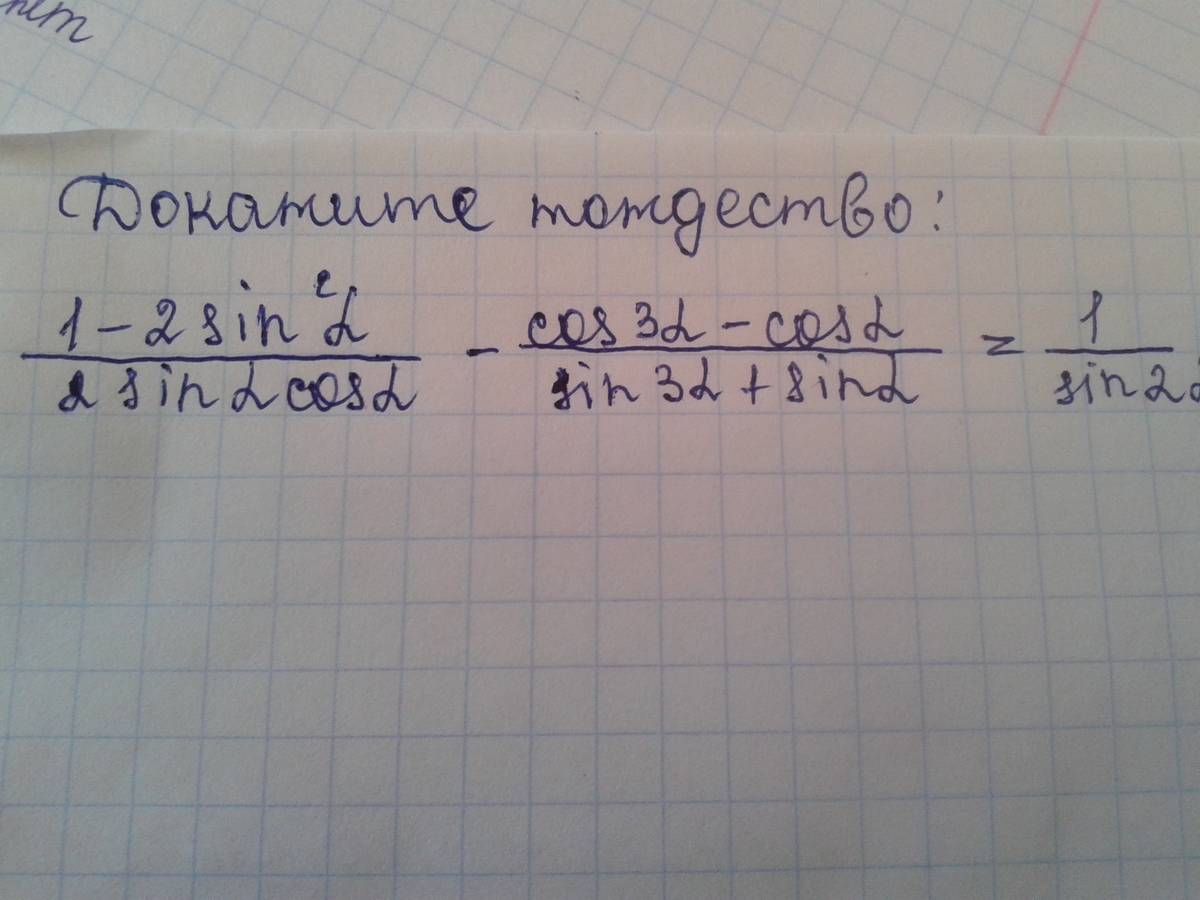
Ответы
Автор ответа:
2
Доказать тождество :
(1 - 2sin²α)/sin2α -(cos3α - cosα)/(sin3α+sinα) =1/sin2α.
--------------------------------------------------------------------------------
(1 - 2sin²α)/sin2α -(cos3α - cosα)/(sin3α+sinα) =
(1 - 2sin²α)/2sinα*cosα - (-2sin2α*sinα)/2sin2α*cosα =
(1 - 2sin²α)/2sinα*cosα +sinα/cosα =(1-2sin²α +2sinα*sinα)/2sinα*cosα =1/sin2α.
************************* использованы формулы ********************************
sin2α =2sinα*cosα ;
cosα - cosβ = -2 sin(α-β)/2 * sin(α+β)/2 ;
sinα + sinβ = 2 sin(α+β)/2 * cos(α-β)/2
(1 - 2sin²α)/sin2α -(cos3α - cosα)/(sin3α+sinα) =1/sin2α.
--------------------------------------------------------------------------------
(1 - 2sin²α)/sin2α -(cos3α - cosα)/(sin3α+sinα) =
(1 - 2sin²α)/2sinα*cosα - (-2sin2α*sinα)/2sin2α*cosα =
(1 - 2sin²α)/2sinα*cosα +sinα/cosα =(1-2sin²α +2sinα*sinα)/2sinα*cosα =1/sin2α.
************************* использованы формулы ********************************
sin2α =2sinα*cosα ;
cosα - cosβ = -2 sin(α-β)/2 * sin(α+β)/2 ;
sinα + sinβ = 2 sin(α+β)/2 * cos(α-β)/2
Похожие вопросы
Предмет: Русский язык,
автор: Verich
Предмет: Русский язык,
автор: Нуженответсрочно
Предмет: Английский язык,
автор: Чипа10
Предмет: Английский язык,
автор: maksimmka04
Предмет: Математика,
автор: 121314151617181927