Предмет: Геометрия,
автор: Авогар
Срочно! Очень нужно! Помогите решить задачу! Площадь р/б трапеции, меньшее основание и высота соответственно равны 120,9 и 8. Прямая, параллельная её основаниям, делит боковую сторону в отношении 5:3, считая от большего основания. Найти длину отрезка, отсекаемого на этой прямой окружностью, вписанной в треугольник, образуемый основанием, боковой стороной и диагональю. Заранее огромнейшее спасибо!!!!
Матов:
каким именно основание большим или меньшим ?
Честно говоря сам не знаю, так написано в условии
перезагрузи страницу если не видно
Ответы
Автор ответа:
1
Для начало найдем большее основание , она равна  , то есть
, то есть  .
.
Угол ,боковая сторона
,боковая сторона  , тогда по теореме косинусов , диагональ
, тогда по теореме косинусов , диагональ 
Так как в задаче не говорится какое именно основание , большее или меньшее?
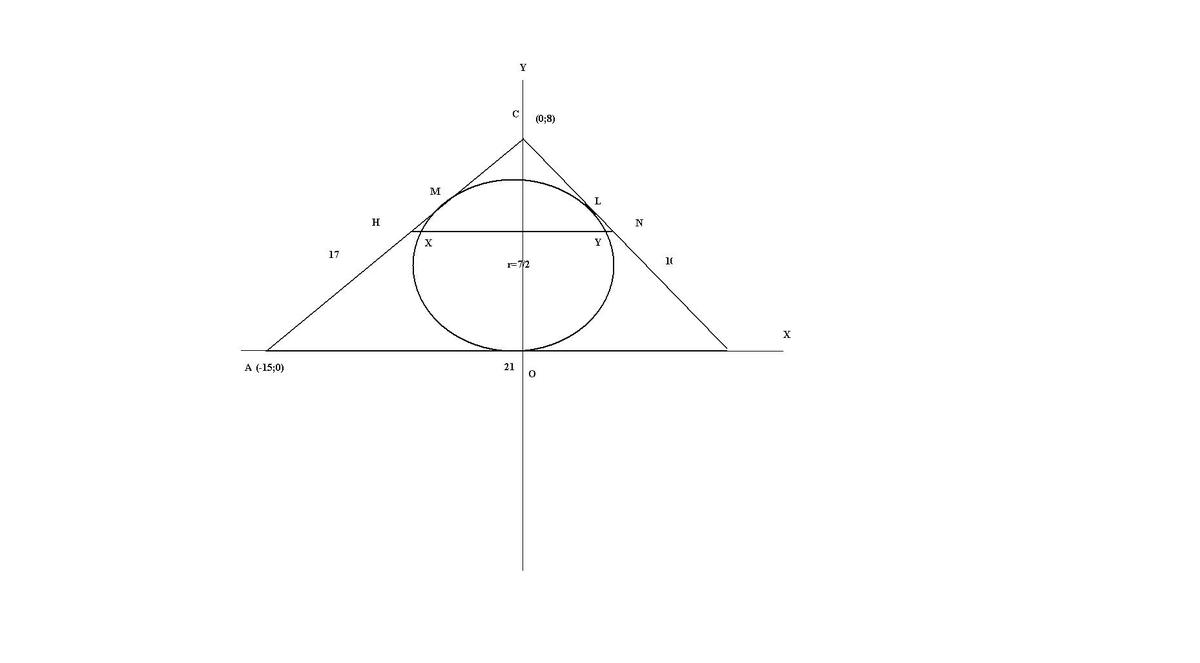
Предположим что большее , тогда так как трапеция равнобедренная отбросим треугольник , и рассмотрим треугольник
, и рассмотрим треугольник  , впишем его в координатную плоскость
, впишем его в координатную плоскость  , так что
, так что  Нам нужно найти
Нам нужно найти 
Радиус вписанной окружности по формуле

Пусть уравнение окружности равна
Уравнения прямых соответственно
Подставляя каждое уравнение прямой , в уравнение окружности и решая ,учитывая то что касательная (стороны ) имеют одну точку касания с окружностью , получаем что (учитываем что дискриминант равен
) имеют одну точку касания с окружностью , получаем что (учитываем что дискриминант равен  )
)
 для
для 


приравниваем
то есть уравнение окружности
Найдем координаты точек

и его уравнение
Решаем систему


Ответ
Угол
Так как в задаче не говорится какое именно основание , большее или меньшее?
Предположим что большее , тогда так как трапеция равнобедренная отбросим треугольник
Радиус вписанной окружности по формуле
Пусть уравнение окружности равна
Уравнения прямых соответственно
Подставляя каждое уравнение прямой , в уравнение окружности и решая ,учитывая то что касательная (стороны
приравниваем
то есть уравнение окружности
Найдем координаты точек
и его уравнение
Решаем систему
Ответ
Приложения:
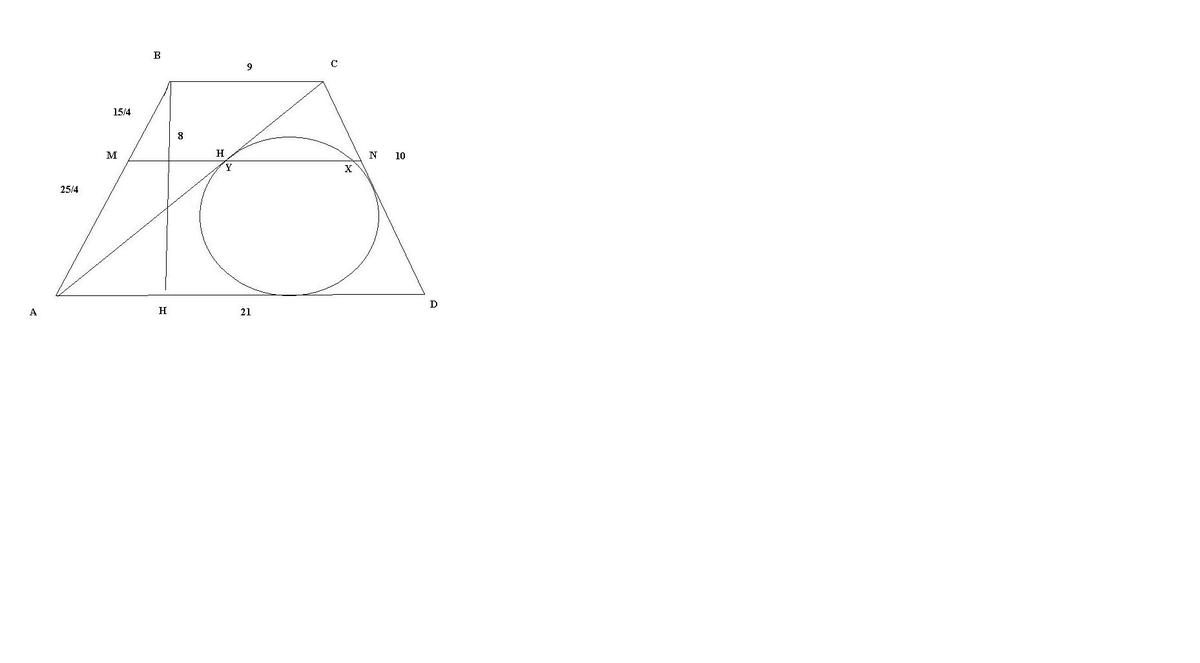
Похожие вопросы
Предмет: Русский язык,
автор: KulakVGulag
Предмет: Русский язык,
автор: 123456gmitri1
Предмет: Русский язык,
автор: зазоша
Предмет: Математика,
автор: julla49
Предмет: Математика,
автор: NIK10000000000