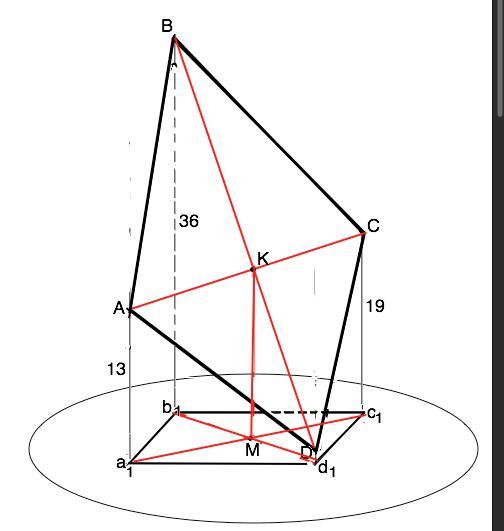
ABCD - параллелограмм, из точек A, B, C, и D на плоскость альфа опущены перпендикуляры.Aa1, Bb1, Cc1, Dd1, Aa1 = 13, Bb1 = 36, Cc1 = 19. Найти Dd1.
Ответы
решение:
Получается, что d = a-b+c.
Исходим из того, что проекцией параллелограмма на плоскость будет также параллелограмм. Ну и там чертим векторы:
Получаем, что АА1+A1B1=AB+BB1, DD1+D1C1=DC+CC1
также имеем равенства (из параллелограммов): A1B1=D1C1, AB=DC
Из всего этого получаем, что DD1=CC1-BB1+AA1. Это все векторные уравнения.
так как все векторы AA1, BB1, CC1 и DD1 однонаправлены, то просто подставляем сюда их длины.
отсюда находим ответ
Объяснение: Принципы решения подобных задач схожи.
Соединим точки а1 и с1, d1 и b1 проекции параллелограмма на плоскости альфа. Соединим А и С, В и D данного по условию параллелограмма АВСD.
Перпендикуляры Аа1 и Сс1, Вb1 и Dd1 параллельны, => четырехугольник а1АСс1 - трапеция. Точки К и М - пересечение диагоналей исходного параллелограмма и его проекции a1b1c1d1 ( тоже параллелограмма) на плоскость альфа, а КМ - их средняя линия.
Диагонали параллелограмма точкой пересечения делятся пополам. Из трапеции Аа1с1С средняя линия КМ=(13+19):2=16
Для трапеции Вb1d1D отрезок КМ - также средняя линия. Средняя линия трапеции равна полусумме оснований. Тогда сумма Вb1+Dd1=KM•2=32. НО! Длина основания Вb1 > 32, т.е. больше суммы оснований трапеции Вb1d1D.
Ясно, что в условии задачи допущена ошибка в длинах перпендикуляров из вершин ABCD, что не помешает при корректных величинах без труда найти четвертый перпендикуляр ( Dd1).