Question

Через две образующие конуса проведена плоскость, пересекающая основание по хорде длиной 8 см. Эта плоскость образует с основанием угол 60 градусов. Вычислите объем конкса, если радиус основания равен 5. С рисунком!

Answer 1

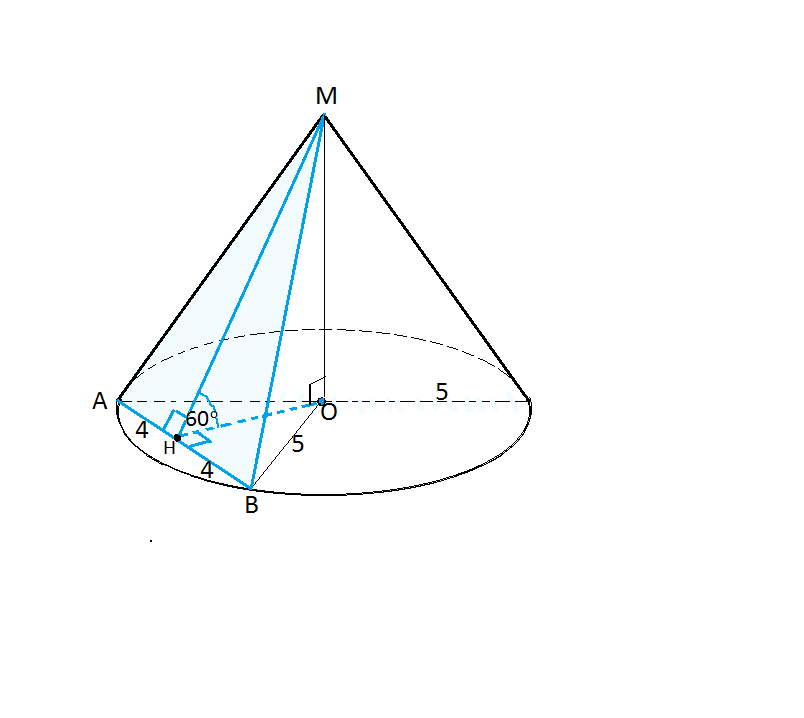
Сечение конуса МАВ, ограниченное двумя образующими и хордой - равнобедренный треугольник.
Его высота МН делит хорду пополам ( на два равных отрезка по 4 см) и образует с основанием угол 60°
ОН⊥хорде АВ. Треугольник ОНВ - египетский ( из отношения катета и гипотенузы).
Следовательно, ОН=3 см
угол НМО равен 30°, гипотенуза МН=2*ОН=6. ⇒
МО=МН*sin 60°=6*√3):2=3√3
Объем конуса найдем по формуле 
V=S*h:3
S=πr²=π*25 см²
V=π*25*(3√3):3=25V=π*25*√3 cм³