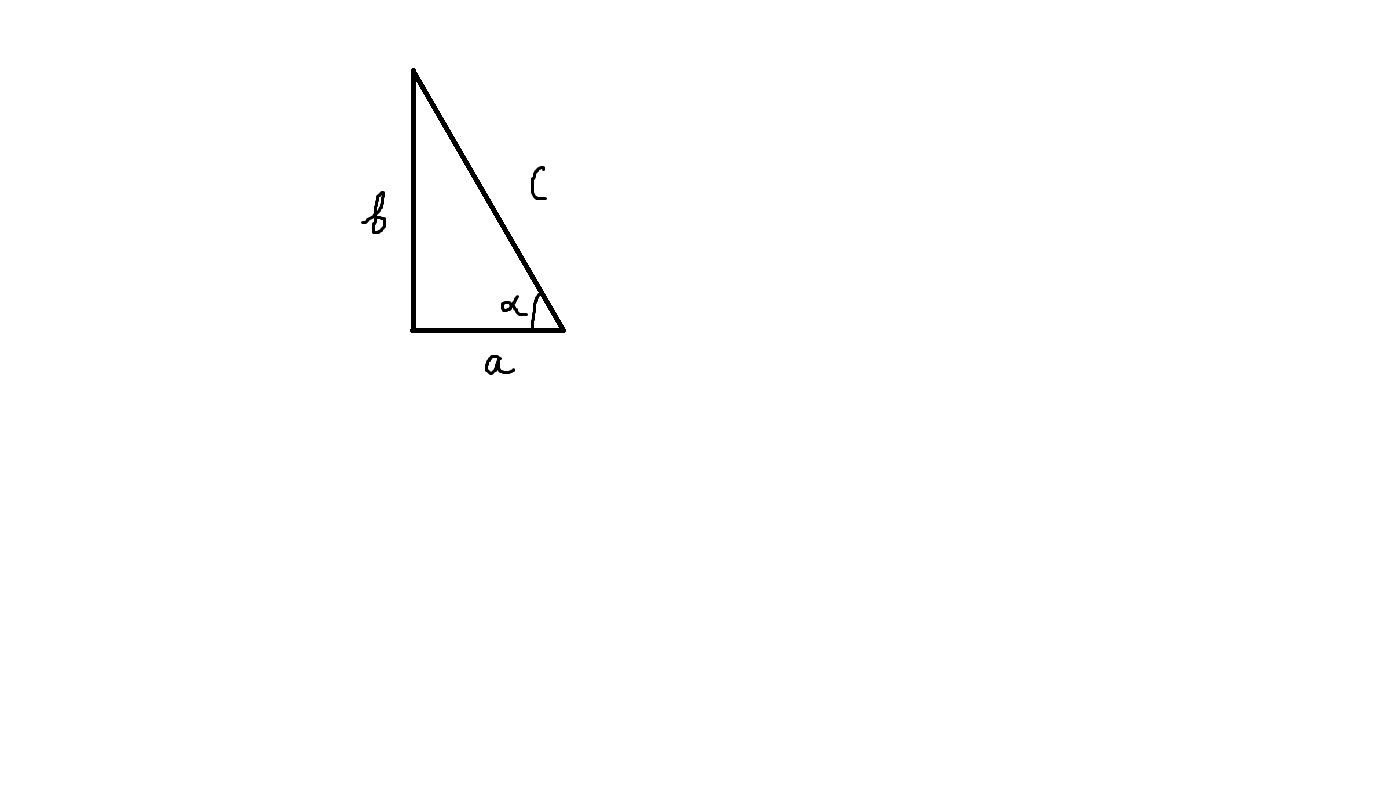ПОМОГИТЕ, СРОЧНО НАДО!РЕШИТЕ ПОЖАЛУЙСТА ЧТО МОЖЕТЕ)зАРАНЕЕ СПАСИБО
1.упростите выражение
ctg(2п+a)*sin(п2+a)
_________________
cos(п-a)*tg(3п2-a)
2.Вычислите значение выражения
16sin12º*cos12º*cos24º
_______________
cos 42º
3.Найдите значение выражение
(ctg(arccos 14))-2(в минус второй)
4.Вычислите
2tg(5п2-a)
__________
5ctg(a+5п) ,если a=5п6
5.Найдите значение выражения
-3sina+4cosa
___________
5cos a+2 sina ,если tg a=-2
6.Упростите выражение cos^2 B+sin ^4B+ sin ^2B+cos^2B
7.Вычислите sin (a+B)-2cosa ,если sin a=1213 , sin B 35, причем a и B углы первой четверти
8. Упростите выражение tg 17º*tg 23º+(tg 17º+tg23º)*ctg 40ºОтветы
1
Здесь заметим, что первый из углов - это 2π или π/2. Значит, воспользуемся формулами приведения:
ctg(2п+a)*sin(п2+a) / (cos(п-a)*tg(3п2-a) = ctg a * cos a / -cos a * ctg a = cos a / -cos a = -1
2
Cначала преобразуем числитель отдельно. Для его преобразований воспользуемся формулами двойного аргумента.
16sin12º*cos12º*cos24º = 8 * 2sin12º*cos12º*cos24º = 8sin 24°cos 24° = 4 * 2sin 24°cos 24° = 4sin 48°
Получим,
4sin 48° / cos 42° = 4sin(90° - 42°) / cos 42° = 4cos 42° / cos 42° = 4
3
Здесь вся сложность заключается в том, чтобы найти точное значение выражения ctg(arccos 1/4). Поэтому для его нахождения воспользуемся методом прямоугольного треугольника(рисунок сейчас приложу). Рассмотрим прямоугольный треугольник.
Пусть arccos 1/4 = α, тогда по определению арккосинуса cosα = 1/4
По сути, как несложно догадаться, нам нужно найти ctg α, зная его косинус.
cos α = a/c
a/c = 1/4, отсюда a = 1, c = 4
ctg α = a/b, не хватает только лишь b. Найдём её по теореме Пифагора,
b² = c² - a²
b² = 16 - 1 = 15
b = √15
Тогда, ctg α = a/b = 1/√15 = √15/15
Но α = arccos 1/4. Значит, ctg(arccos 1/4) = √15/15
Теперь осталось только верно посчитать:
2⁻² = 1/4
√15 / 15 - 1/4 = (2√15 - 15 )/ 60