Question

Найдите площадь трапеции если ее основания 5 см , 17 см , а боковые стороны соотвецтвенно равны 20 см и 16 см . Помогите пожалуйста

Answer 1

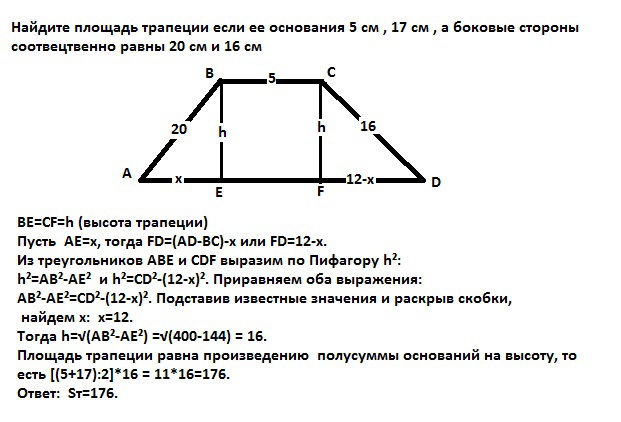
ВЕ=СF=h (высота трапеции)
Пусть  АЕ=х, тогда FD=(AD-BC)-x или FD=12-x.
Из треугольников АВЕ и CDF выразим по Пифагору h²:
h²=AB²-AE²  и h²=CD²-(12-x)². Приравняем оба выражения:
AB²-AE²=CD²-(12-x)². Подставив известные значения и раскрыв скобки,
 найдем х:  х=12см.
Тогда h=√(AB²-AE²) =√(400-144) = 16cм.
Площадь трапеции равна произведению  полусуммы оснований на высоту, то есть [(5+17):2]*16 = 11*16=176см².
Ответ:  Sт=176см².