Question

1.В параллелограмме ABCD AD=12см, AB=6см, уголBAD=60градусов.
Биссектриса угла D пересекает BC в точке  Е.
    1)найдите высоты параллелограмма и его площадь.
     2)определите вид треугольника ECD и найдите длину описанной около тругольника окружности.
    3)найдите длину большей диагонали параллелограмма.

Answer 1

1.
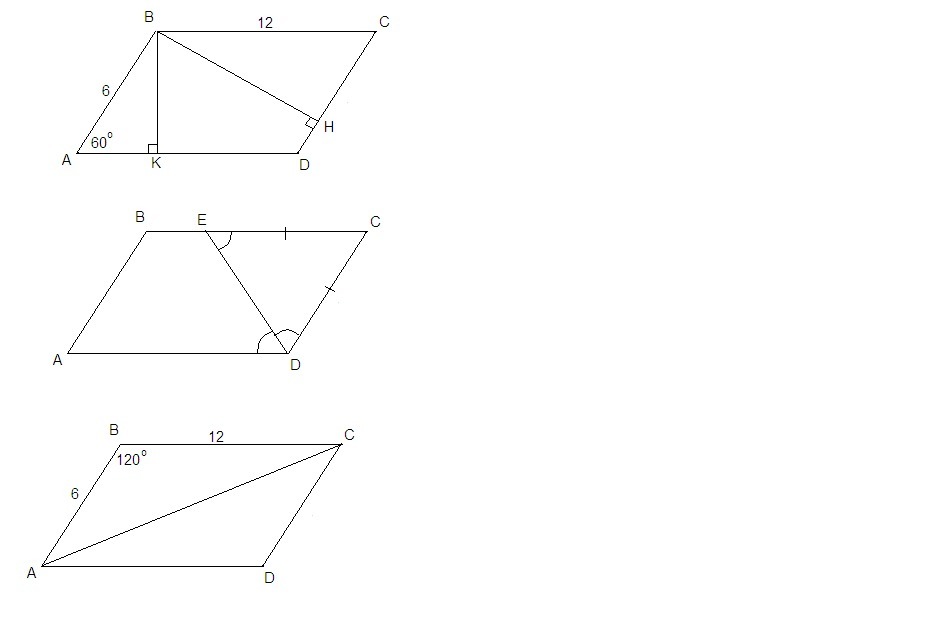
ΔАВК: ∠АКВ = 90°
             ВК = АВ · sin60° = 6 · √3/2 = 3√3 см
ΔСВН: ∠СНВ = 90°, ∠ВСН = ∠BAD = 60° как противолежащие углы параллелограмма.
              ВН = ВС · sin 60° = 12 · √3/2 = 6√3 см
Sabcd = AD · BK = 12 · 3√3 = 36√3 см²

2.
∠ADE = ∠CED как накрест лежащие при пересечении ВС║AD секущей DE.
∠ADE = ∠CDE так как DE биссектриса, ⇒
∠CED = ∠CDE.
ΔECD равнобедренный с углом 60° при вершине, значит
ΔECD равносторонний.

3.
ΔАВС: по теореме косинусов:
AC² = AB² + BC² - 2AB·BC·cosB
∠ABC = 180° - ∠BAC = 120° так как сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.
AC² = 36 + 144  - 2 · 6 · 12 · (- 0,5)
AC² = 180 + 72 = 252
AC = √252 = 2√63 см