Предмет: Геометрия,
автор: BJIADA
ПОМОГИТЕ, ПОЖАЛУЙСТА
Отрезок AC - диаметр окружности, AB - хорда, MA - касательная, угол MAB острый. Докажите, что <MAB=<ACB
< - угол
желательно с рисунком.
Ответы
Автор ответа:
3
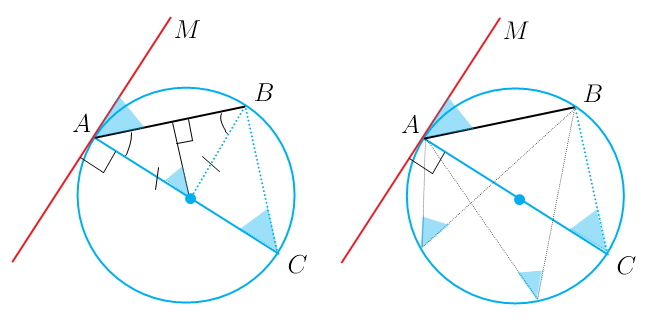
можно воспользоваться теоремой:
Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
это легко доказывается...
достаточно рассмотреть равнобедренный треугольник с вершиной в центре окружности и боковыми сторонами-радиусами окружности
угол при основании этого треугольника в сумме с углом МАВ составляет 90°
и, следовательно, равен половине угла при вершине ---центрального угла, градусная мера которого и определяет градусную меру дуги АВ)))
угол АСВ --вписанный, опирается на дугу АВ, равен половине градусной меры дуги АВ
угол МАВ равен (по теореме) половине градусной меры дуги АВ
интересно, что АС не обязательно должен быть диаметром)))
это видно на втором рисунке
угол МАВ (угол между касательной и секущей) равен любому вписанному и опирающемуся на дугу АВ углу...
Угол, образованный касательной к окружности и секущей, проведенной через точку касания, равен половине дуги, заключенной между его сторонами.
это легко доказывается...
достаточно рассмотреть равнобедренный треугольник с вершиной в центре окружности и боковыми сторонами-радиусами окружности
угол при основании этого треугольника в сумме с углом МАВ составляет 90°
и, следовательно, равен половине угла при вершине ---центрального угла, градусная мера которого и определяет градусную меру дуги АВ)))
угол АСВ --вписанный, опирается на дугу АВ, равен половине градусной меры дуги АВ
угол МАВ равен (по теореме) половине градусной меры дуги АВ
интересно, что АС не обязательно должен быть диаметром)))
это видно на втором рисунке
угол МАВ (угол между касательной и секущей) равен любому вписанному и опирающемуся на дугу АВ углу...
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: JungKookiiiii
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: fatimarukir
Предмет: Математика,
автор: Sadadi
Предмет: Математика,
автор: Valentarg