Предмет: Алгебра,
автор: Зубарев
В картинке сама задача. 10-ый класс, уравнение.
Приложения:
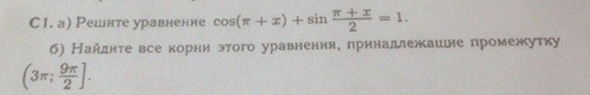
Ответы
Автор ответа:
1
Отбор корней
Для корня x=π/3 + 2πn
n=2; x=13π/3
Для корня x=-π/3 + 2πn
n=2; x=11π/3
Зубарев:
Спасибо, это не обязательно.
Похожие вопросы
Предмет: Английский язык,
автор: blackpink94
Предмет: Английский язык,
автор: AngelOfBTS
Предмет: Русский язык,
автор: sxeccbhujib
Предмет: Физика,
автор: MopHoMup
Предмет: Биология,
автор: sirious12