Предмет: Геометрия,
автор: loooool814
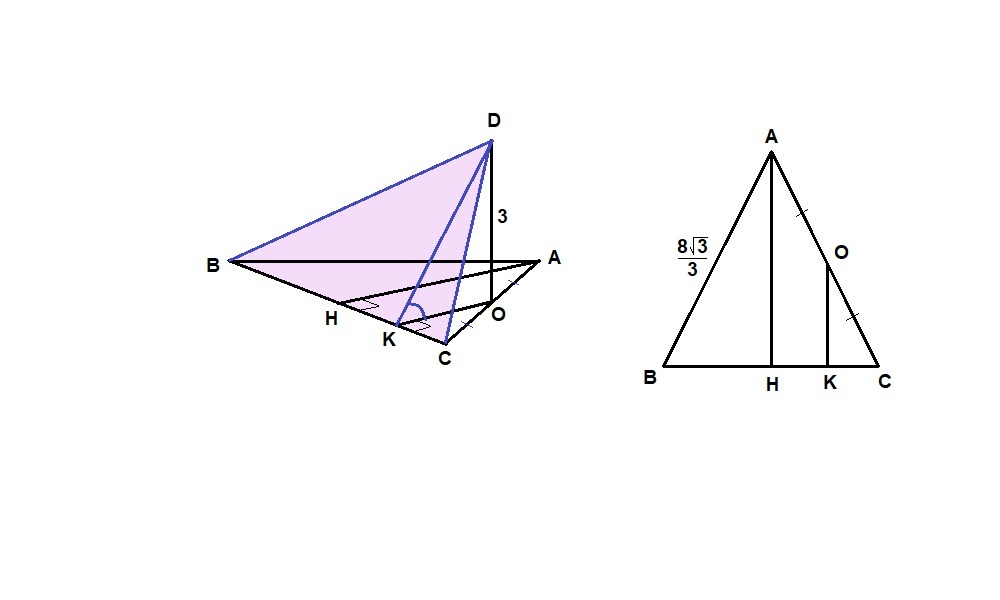
ABC правильный треугольник, О середина AC, OD перпендикулярно ABC, OD=3. Сторона треугольника равна 8 корней из 3 разделить на 3. Найдите угол между плоскостями ABC и CBD
Ответы
Автор ответа:
2
Пусть Н - середина ВС. Тогда АН - медиана и высота равностороннего треугольника АВС.
По формуле высоты равностороннего треугольника:
АН = АВ√3/2 = 8√3/3 · √3 / 2 = 4.
Проведем ОК║АН. Тогда ОК⊥ВС. ОК - проекция DK на плоскость АВС, значит и DK⊥BC по теореме о трех перпендикулярах.
∠DKO - линейный угол двугранного угла между плоскостями АВС и DBC - искомый.
Так как О - середина АС и ОК║АН, то ОК - средняя линия треугольника АНС (по признаку).
ОК = 1/2 АН = 4/2 = 2.
ΔDOK: ∠DOK = 90°,
tg∠DKO = DO / OK = 3/2
∠DKO = arctg(3/2)
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: JjjjjeeeeeyyyylllllO
Предмет: Английский язык,
автор: Вопросик002
Предмет: Русский язык,
автор: Игорь981
Предмет: Геометрия,
автор: Аноним