Предмет: Геометрия,
автор: Dashunya2508
Помогите решить задачу!!!!!
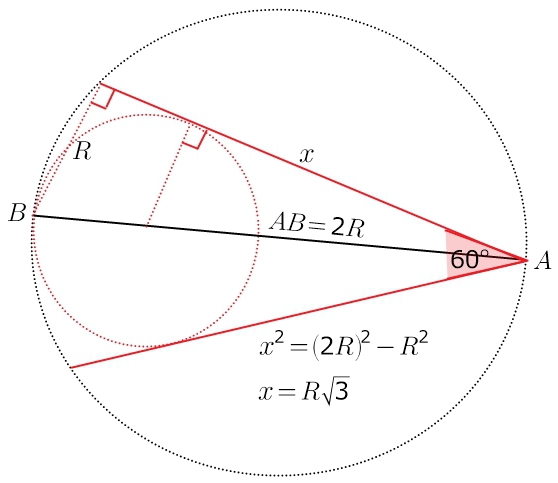
Две окружности касаются внутренне в точки В, АВ - диаметр большой окружности. Через точку А проведены две хорды, которые касаются меньшей окружности. Угол между двумя хордами равен 60*. Найдите длины этих хорд если радиус большей окружности равен R.
Ответы
Автор ответа:
3
эти хорды будут равны, т.к.
они образуют два равных (по гипотенузе и катету) прямоугольных (опирающихся на диаметр) треугольника
диаметр будет биссектрисой угла между хордами
(((отрезки касательных из одной точки равны)))
катет против угла в 30 градусов равен половине гипотенузы...
они образуют два равных (по гипотенузе и катету) прямоугольных (опирающихся на диаметр) треугольника
диаметр будет биссектрисой угла между хордами
(((отрезки касательных из одной точки равны)))
катет против угла в 30 градусов равен половине гипотенузы...
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: поля875
Предмет: Другие предметы,
автор: schooll13
Предмет: Русский язык,
автор: kirapalenlova0
Предмет: Русский язык,
автор: ШкололоМЭН
Предмет: Физика,
автор: gul4ik4