Question

Радиусы двух кругов равны 27 и 13, а расстояние между их центрами равно 50. Найти длины их общих касательных (внешней и внутренней).

 

Answer 1

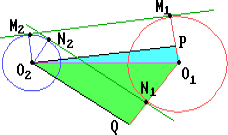
Пусть O1 и O2 — центры окружностей, M1 и M2 — точки касания с внешней касательной, N1 и N2 — с внутренней, P — основание перпендикуляра, опущенного из O2 на O1M1. Тогда

 M1M22 = O1O22 - O1P2 = 502 - (27 - 13)2 = 482.

 

Пусть Q — основание перпендикуляра, опущенного из O1 на продолжение радиуса O2N2. Тогда

 N1N22 = O2Q2 = O1O22 - O1Q2 = 502 - (27 + 13)2 = 302

 

Ответ...48 и 30.