Предмет: Алгебра,
автор: sushivasabi77
Помогите пожалуйста
Номер 1192 и 1198
Очень нужно
Заранее спасибо))
Приложения:
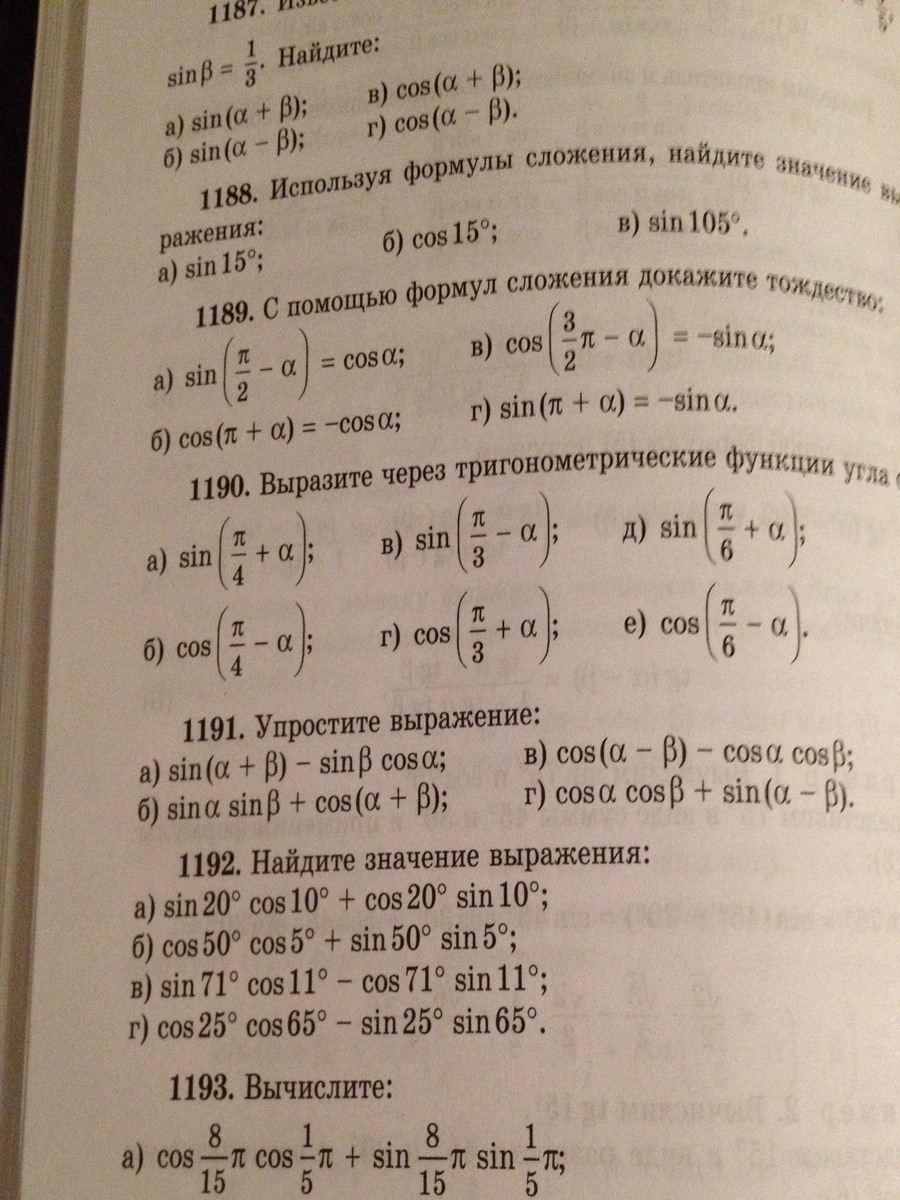
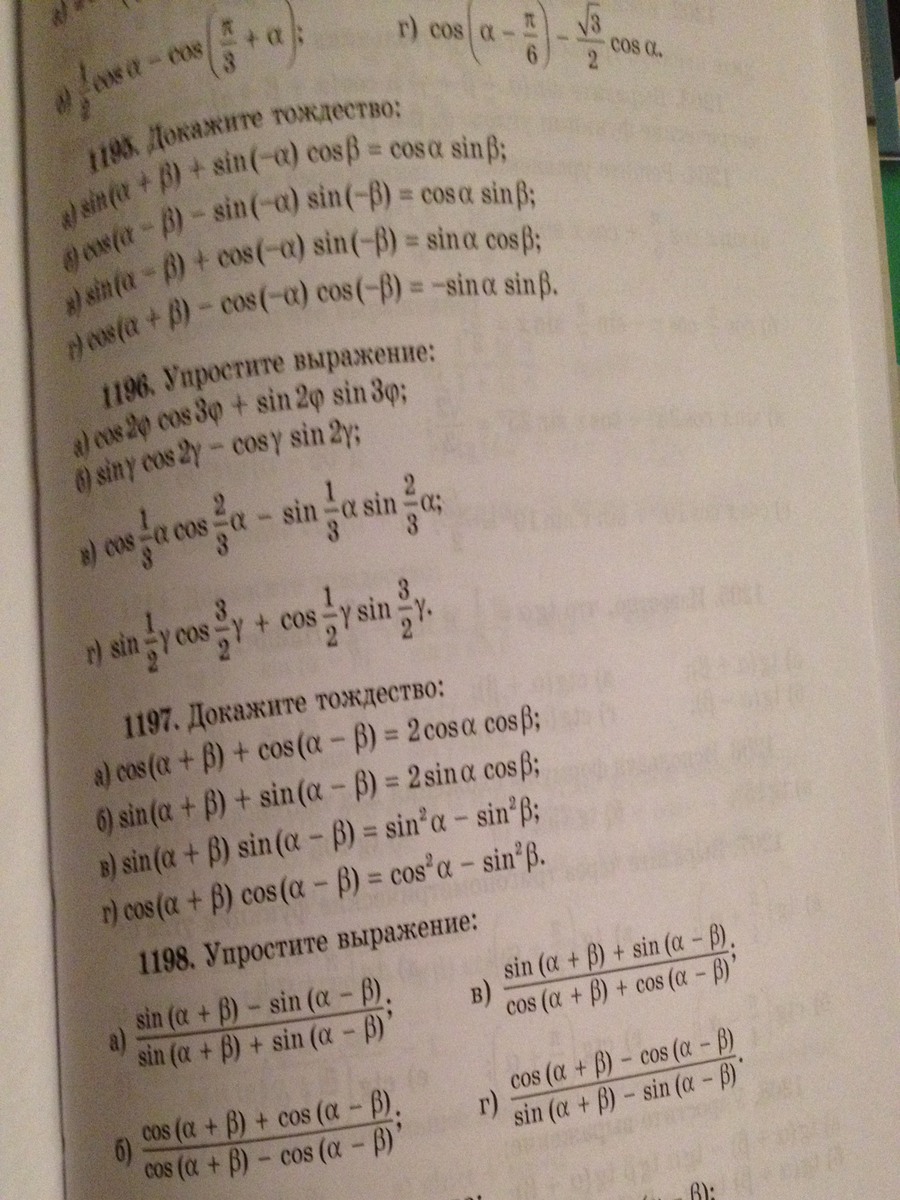
Ответы
Автор ответа:
3
sin20cos10 + cos20sin10 = sin(20+10)
cos50cos5 + sin50sin5 = cos(50+5)
sin71cos11 - cos71sin11 = sin(71-11)
cos25cos65 - sin25sin65 = cos(25-65)
sin (a+b) - sin(a-b) = sinAcosB+cosAsinB - sinAcosB - cosAsinB
sin (a+b) - sin (a-b) sinAcosB+cosAsinB - sinAcosB - cosAsinB
Дальше сама по формулам там похоже
cos(a+b)=cosA+cosB-sinA+sinB
cos(a-B)=cosAcosB+sinAsinB
sin(a+b)=sinAcosB+cosAsinB
sin(a-b)=sinAcosB-cosAsinB
cos50cos5 + sin50sin5 = cos(50+5)
sin71cos11 - cos71sin11 = sin(71-11)
cos25cos65 - sin25sin65 = cos(25-65)
sin (a+b) - sin(a-b) = sinAcosB+cosAsinB - sinAcosB - cosAsinB
sin (a+b) - sin (a-b) sinAcosB+cosAsinB - sinAcosB - cosAsinB
Дальше сама по формулам там похоже
cos(a+b)=cosA+cosB-sinA+sinB
cos(a-B)=cosAcosB+sinAsinB
sin(a+b)=sinAcosB+cosAsinB
sin(a-b)=sinAcosB-cosAsinB
sushivasabi77:
спасибо
Похожие вопросы
Предмет: Немецкий язык,
автор: CCQ
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: sacredand
Предмет: Биология,
автор: CrystalKe
Предмет: География,
автор: svetlano49