Предмет: Алгебра,
автор: zasadaza
я не знаю что делать... помогайте друзья, уж очень нужно! нужно найти значение выражения.Это вообще реально?!
Приложения:
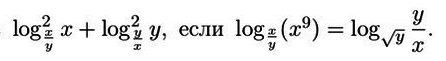
Ответы
Автор ответа:
0
t=Loq_(x) y
Loq²_(x/y) x =(1/Loq_(x) (x/y))² =1/(1 - Loq_(x) y)² =1/(1-t)² ;
Loq² _(y/x) y =(1/Loq _(y) (y/x))² =1/(1 -Loq_(y) x)² =1/(1 -1/Loq_(x) )² =1/(1 -1/t)² =
=t²/(1-t)².
Loq²_(x/y) x +Loq² _(y/x) y =1/(1-t)² +t²/(1-t)² = (1+t²)/(1-t)² (1).
***********************************************************************************
Loq _(x/y) (x)^9 = 9Loq_(x/y) (x) = 9/Loq_x (x/y) =9/(1 -Loq_x y) =9/(1-t)
Loq_(√y) (y/x) =1/2* Loq_(y) (y/x) =1/2*(1 -Loq_(y) x) =1/2*( 1 -1/Loq _(x) y) =
=(Loq_(x) y -1)/2Loq_(x) y) =(t-1)/2t.
9/(1 -t) = (t-1)/2t ⇒ t = . . . и поставить в (1)
*** нужно на бумаге ***
Loq²_(x/y) x =(1/Loq_(x) (x/y))² =1/(1 - Loq_(x) y)² =1/(1-t)² ;
Loq² _(y/x) y =(1/Loq _(y) (y/x))² =1/(1 -Loq_(y) x)² =1/(1 -1/Loq_(x) )² =1/(1 -1/t)² =
=t²/(1-t)².
Loq²_(x/y) x +Loq² _(y/x) y =1/(1-t)² +t²/(1-t)² = (1+t²)/(1-t)² (1).
***********************************************************************************
Loq _(x/y) (x)^9 = 9Loq_(x/y) (x) = 9/Loq_x (x/y) =9/(1 -Loq_x y) =9/(1-t)
Loq_(√y) (y/x) =1/2* Loq_(y) (y/x) =1/2*(1 -Loq_(y) x) =1/2*( 1 -1/Loq _(x) y) =
=(Loq_(x) y -1)/2Loq_(x) y) =(t-1)/2t.
9/(1 -t) = (t-1)/2t ⇒ t = . . . и поставить в (1)
*** нужно на бумаге ***
zasadaza:
сильно задолбался?
ща нао сообразить че к чему)
какой ответ получается? в итоге?
во второй строчке пропущена буква
Похожие вопросы
Предмет: Английский язык,
автор: mightwood1337
Предмет: Українська мова,
автор: sashasevsova
Предмет: Английский язык,
автор: mightwood1337
Предмет: Математика,
автор: siya17
Предмет: Физика,
автор: fiigovomnrcnatnado