Предмет: Алгебра,
автор: Labirint
Решите, пожалуйста, выражение:
Приложения:
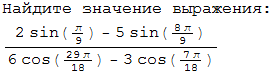
Ответы
Автор ответа:
0
Для начала упростим то, что самое сложное. Заметим, что
Формула синуса разности углов
Формула косинуса разности углов
Подставим, полученные выраңения в исходное выражение
Теперь попытаемся упростить то, что в знаменателе
Формула коинуса разности углов
Возвращаясь к исходной формууле,
Ответ: -1.
Похожие вопросы