Question

1 сторона ромба =13, 1 с диагоналей =10, найти вторую диагональ
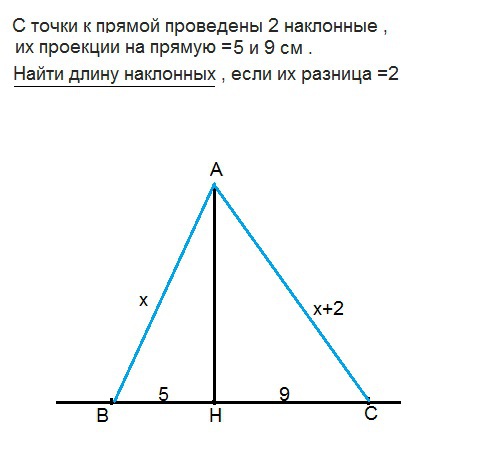
С точки к прямой проведены 2 наклонные , их проекции на прямую =5 и 9 см . Найти длину наклонных , если их разница =2

Answer 1

1) Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Т.к. в ромбе все стороны равны, то
d²+D²=4a²
100+D²=4*169
D²=676-100
D=√576
D=24
-------------
2)Проекция наклонной - это расстояние от основания этой наклонной до основания перпендикуляра, опущенного из другого конца наклонной на прямую, к которой наклонная проведена.
Так как наклонные проведены из одной точки, перпендикуляр от этой точки  общий для для обеих наклонных.
Пусть эти наклонные будут АВ и АС, перпендикуляр - АН.
Соединив В и С, получим треугольник АВС с высотой АН.
По условию ВН=5, СН=9, АС-АВ=2
Обозначим длину АВ х.
Тогда АС=х+2
Выразим АН² по т. Пифагора из треугольника АНВ,
АН²=х²-25АН², 
АН ², выраженная по т. Пифагора из треугольника АНС
АН²=(х +2)²-81
Приравняем эти два уравнения, т.к. они выражают одну величину. 
х²-25=х²-4х+81
4х=77-25
х=52:4
х=13
АВ=13
АС=13+2=15