Предмет: Геометрия,
автор: AlexandraL11
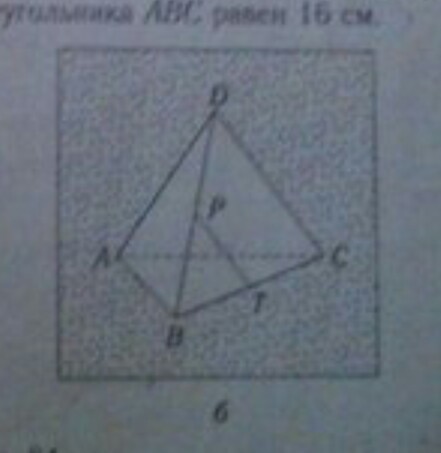
На рисунке 84 б изображён правильный тэдраэтр DABC . Площадь полной поверхности которого равна 16/3см (/ - корень). Точки Р и Т - середины рёбер BD и BC соответственно. В треугольник PBT вписана окружность.
Вычислить дугу длины окружности, меньшую 180 градусов, концами которой являются точки касания окружности с рёбрами BD и BC.
Приложения:
cos20093:
а что, PBT уже НЕ правильный треугольник? И причем тут площадь?
Ну собственно, площадь PBT = √3; откуда его сторона 2; (ребро тетраэдра = 4); радиус вписанной окружности 1/√3; и надо найти ТРЕТЬ длины окружности с таким радиусом. Это π/9. Я конечно могу и ошибаться.
Кстати, легко можно увидеть, что если провести ВСЕ средние линии граней, то получится ровно 16 одинаковых треугольников.
Ответы
Автор ответа:
13
1) CDB подобен BPT, K=1/2 PT=BP=BT=1/2a, где а-сторона тетраэдра.
2) Sполн=a^2корень3 (по формуле), отсюда а=4.
3) r окр. впис. в BPT =b/2корень3, где b-сторона BPT, b=1/2a, отсюда r=1/корень3.
4) Угол P1OT1, О-центр окр., P1 и T1 -точки касания, равен 120 град.
5) L=пr120/180, L=2п/3корень3.
2) Sполн=a^2корень3 (по формуле), отсюда а=4.
3) r окр. впис. в BPT =b/2корень3, где b-сторона BPT, b=1/2a, отсюда r=1/корень3.
4) Угол P1OT1, О-центр окр., P1 и T1 -точки касания, равен 120 град.
5) L=пr120/180, L=2п/3корень3.
Похожие вопросы
Предмет: Українська мова,
автор: Аноним
Предмет: Другие предметы,
автор: sbsnizanka295
Предмет: Русский язык,
автор: d7184484
Предмет: Алгебра,
автор: qqqqq3327