Предмет: Алгебра,
автор: Аноним
Решите уравнение! 60 ПНКТ за лучшее решение!
1)sin(x-π/4)=0
2)tg4x=√3
3)sinx(3x+π/3)=1
4)cos3x=1/2
5)tg(x-π/6)=-√3
Ответы
Автор ответа:
0
1)sin(x-π/4)=0
x-pi/4 = pi*k , k - Z
x=pi/4 +pi*k , k - Z
2)tg4x=√3
4x=pi/3 + 2*pi*k, k - Z
x=pi/12 * pi*k/2 , k - Z
3)sinx(3x+π/3)=1
3x+pi/3=pi/2+2*pi*k , k - Z
x=pi/18+2*pi*k/3 , k - Z
4)cos3x=1/2
3x=+-pi/3+2*pi*k , k - Z
x=+-pi/9+2*pi*k/3 , k - Z
5)tg(x-π/6)=-√3
x-pi/6=-pi/3+2*pi*k , k - Z
x=-pi/6 + 2*pi*k , k - Z
Автор ответа:
0
1)sin(x-pi/4)=0
t=x-pi/4
sint=0
1.t=0+2pi*k
x-pi/4=0
x=pi/4
2.t=pi+2pi*k
pi=x-pi/4
x=5pi/4+2pi*k
3)sinx(3x+pi/3)=1
t=3x+pi/3
sint=1
t=pi/2
3x+pi/3=pi/2
x=pi/18
5)tg(x-pi/6)=-√3
t=x-pi/6
tgt=-√3
t=-pi/3+2pi*k . k=Z
t=2pi/3+2pi*k . k=Z
Приложения:
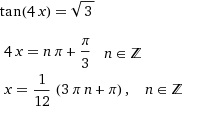
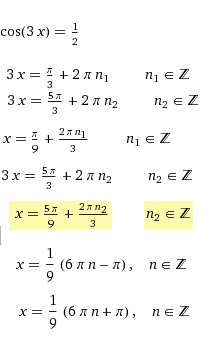
Похожие вопросы
Предмет: Химия,
автор: sansskeleton1999
Предмет: География,
автор: ssohakimova
Предмет: Английский язык,
автор: absametbirhanym98
Предмет: Физика,
автор: Nls