Question

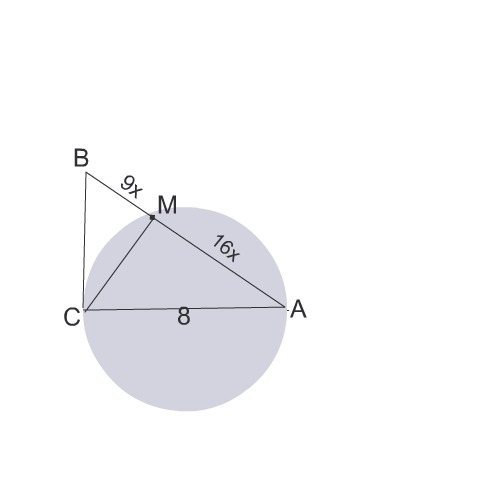
помогите решить задачу,пожалуйста! Длина катета АС прямоугольного треугольника АВС равна 8см. Окружность с диаметром АС пересекает гипотенузу АВ в точке М.Найти площадь треугольника АВС, если известно,что АМ:МВ=16:9

Answer 1

Сделаем рисунок к задаче.

Рассмотрим ⊿ АМС. Этот треугольник прямоугольный, т.к. АС - гипотенуза треугольника - диаметр окружности.

Следовательно, СМ - высота ⊿ АВС.

Известно, что катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой.

АС²=АМ·АВ

Пусть х - коэффициент отношения отрезков гипотенузы.
тогда
64=16·(16+9)х²
400х²=64

х²=0,16
х=0,4
АВ=0,4·25=10
ВС=6 ( по теореме Пифагора)
S АВС=АС·ВС:2

S= 8·6:2=24 см²