Помогите пожалуйста ,уже отправляю второй раз,решить задания под № 3, №4- найти площадь четырехугольников!!!
Ответы
Задача 1.
Площадь прямоугольника равна произведению его сторон.
СД=1/2 АС=4
АD=√ (АС² - СD²)=√ (64-16)=4√ 3
S ABCD=4∙4√3=16√3
Задача 2.
АС - диагональ квадрата.
АВ=АС*sin (45°)=(4√2):2=2√2
S ABCD=AB∙AD=(2√2)²=8
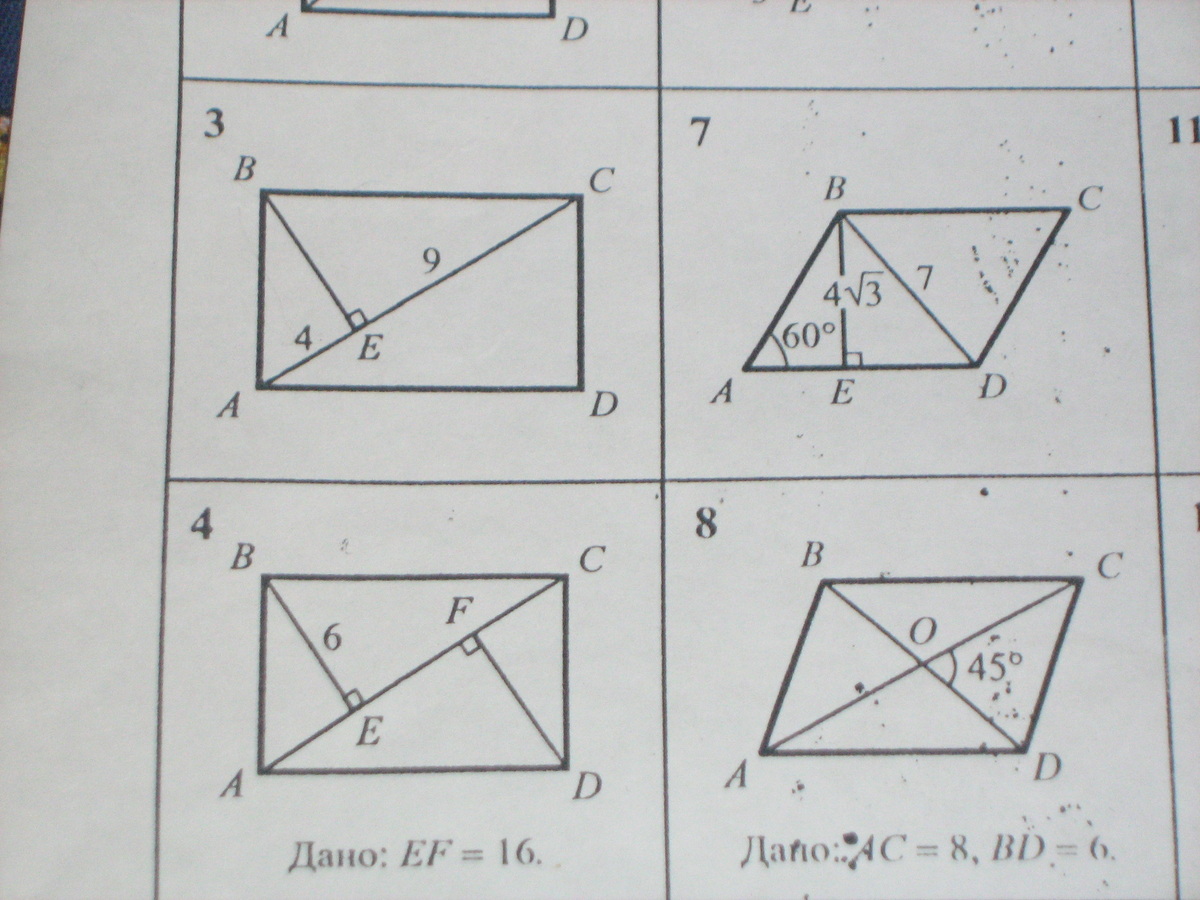
Задача 3.
Площадь прямоугольника равна двум площадям треугольника АВС
Высота ВЕ этого прямоугольного треугольника, проведенная из вершины прямого угла, - среднее пропорциональное между отрезками, на которые делится гипотенуза АС высотой ВЕ.
ВЕ²=АЕ∙ЕС=4∙9=36
ВЕ=√36=6
S ABCD=2 ∙ S ᐃ ABC=ВE ∙AC=6 ∙13= 78
Задача 4. слегка усложненный вариант задачи 3.
АЕ=FC=х
АС=ЕF+АЕ+FC=16+2х
ВЕ²=АЕ∙ЕС
36=х∙(16+х)
36=х² +16х
х² +16х -36=0
D=b²-4ac=16²-4·1·-36=400
x₁=2
х₂= - 18 (не подходит)
S ABCD = 2 ∙ S ᐃ ABC=ВE ∙AC=6∙(ЕF+АЕ+FC)=6∙(16+4)=120
Задача 5.
Площадь параллелограмма равна произведению смежных сторон параллелограмма на синус угла между ними
S ABCD=АВ ∙АD ∙sin (60°)=10∙15∙ √3):2=75√3
Задача 6.
Треугольника АВЕ - египетский с отношением сторон 3:4:5
Высота ВЕ=4 ( можно и по теореме Пифагора найти)
Площадь параллелограмма равна произведению высоты на сторону, к которой она проведена.
S ABCD=ВЕ∙АD=4∙8=32