Предмет: Геометрия,
автор: Аноним
Пожалуйста очень надо с рисунком! !! Высота четырехугольной пирамиды равна 6 см, боковая ее грань наклонена к плоскости основания под углом 45 градусов найти: а) площадь боковой поверхности ; б) площадь полной поверхности. Буду очень признателен!
Ответы
Автор ответа:
8
Решение для правильной четырехугольной пирамиды:
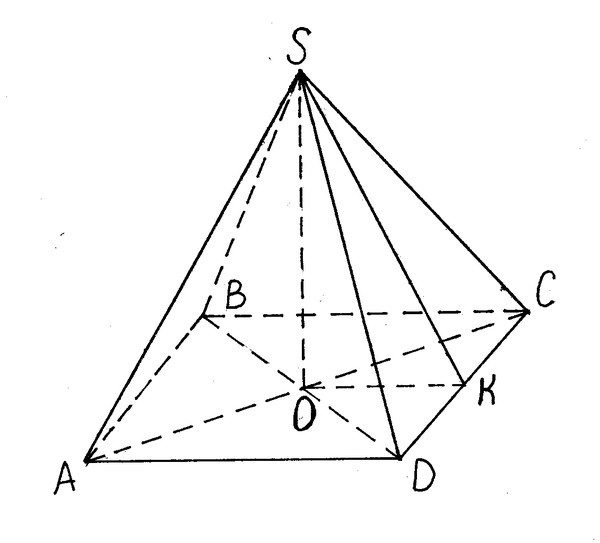
Высота SO=6, <SKO=45°
Из прямоугольного ΔSKO: <SOK=90 °, <SKO=<OSK=45°. Значит ΔSKO - равнобедренный ОК=SO=6, SК=√(ОК²+SО²)=√72=6√2 см
Сторона основания (квадрата) АВ=ВС=СД=АД=2ОК=2*6=12 см, площадь основания Sосн=12²=144
Площадь боковой поверхности Sбок=4S=4*SК*СД/2=2*6√2*12=144√2
Площадь полной поверхности Sполн=Sбок+Sосн=144√2+144=144(√2+1)≈347,65 см
Высота SO=6, <SKO=45°
Из прямоугольного ΔSKO: <SOK=90 °, <SKO=<OSK=45°. Значит ΔSKO - равнобедренный ОК=SO=6, SК=√(ОК²+SО²)=√72=6√2 см
Сторона основания (квадрата) АВ=ВС=СД=АД=2ОК=2*6=12 см, площадь основания Sосн=12²=144
Площадь боковой поверхности Sбок=4S=4*SК*СД/2=2*6√2*12=144√2
Площадь полной поверхности Sполн=Sбок+Sосн=144√2+144=144(√2+1)≈347,65 см
Приложения:
Аноним:
Спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: школа847
Предмет: Русский язык,
автор: Miron2345
Предмет: Английский язык,
автор: austinova578
Предмет: Физика,
автор: Maxonpirat
Предмет: История,
автор: Алексей22843