Предмет: Геометрия,
автор: stormboyzbim
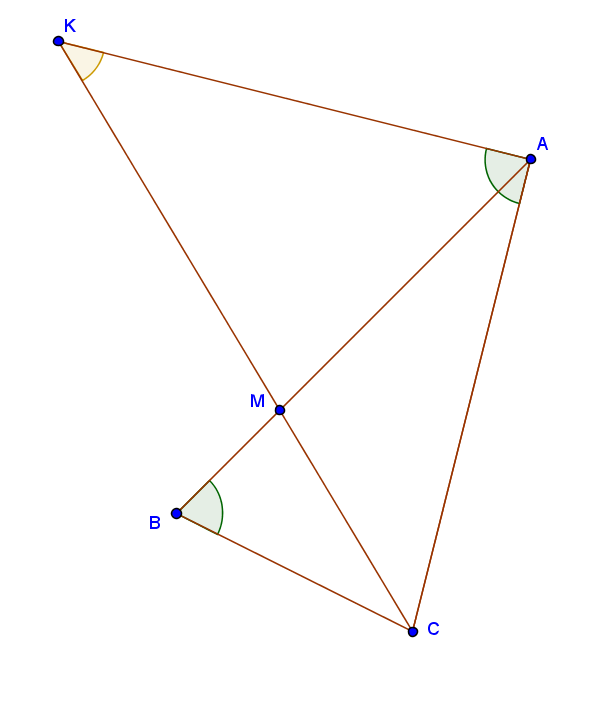
24 задание помоги пожалуйста.
Приложения:

Ответы
Автор ответа:
1
Честно говоря я увидел 2 хода решения задачи:
1) С коэффициентом подобия
2) С коэффициентом подобия
Какой из них правильный сказать наверняка не могу, т.к. не вижу противоречий ни в том, ни в другом.
Собственно ход мыслей таков:
Треугольники подобны по условию, в тр. ABC известны все стороны, в тр. KAC известна 1 сторона (AC=10). При этом сказано, что AC не наибольшая из сторон в тр. AKC (т.к. наибольший угол по условию - KAC).
Решение 1:
Пусть коэффициент подобия равен , тогда
, тогда
KC=
KA=18
По т. косинусов:

Отсюда CosAKC=
Решение 2:
Пусть коэффициент подобия равен , тогда
, тогда
KC=
KA=
По т. косинусов:

Отсюда CosAKC=
За вычислительные ошибки ответственности не несу.
1) С коэффициентом подобия
2) С коэффициентом подобия
Какой из них правильный сказать наверняка не могу, т.к. не вижу противоречий ни в том, ни в другом.
Собственно ход мыслей таков:
Треугольники подобны по условию, в тр. ABC известны все стороны, в тр. KAC известна 1 сторона (AC=10). При этом сказано, что AC не наибольшая из сторон в тр. AKC (т.к. наибольший угол по условию - KAC).
Решение 1:
Пусть коэффициент подобия равен
KC=
KA=18
По т. косинусов:
Отсюда CosAKC=
Решение 2:
Пусть коэффициент подобия равен
KC=
KA=
По т. косинусов:
Отсюда CosAKC=
За вычислительные ошибки ответственности не несу.
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Русский язык,
автор: VovaMel2017
Предмет: Другие предметы,
автор: Аноним
Предмет: Математика,
автор: videofan64
Предмет: Українська мова,
автор: Ghost099